线性回归
主要内容如下:
- 回归和分类的区别
- 线性回归
- 最小二乘法
- 梯度下降法
回归和分类
回归和分类一样,都是对变量进行预测
回归是对连续型变量进行预测,回归预测建模是指建立输入变量X映射到连续输出变量Y的映射函数f
分类是对离散型或连续型变量进行预测,分类预测建模是指建立输入变量X映射到离散输出变量Y的映射函数f
比如,预测天气温度是回归问题,预测天气是下雨还是晴天就是分类问题
线性回归
线性回归(linear regression)是以线性模型来建模自变量和因变量之间关系的方法
\[ y=h(x;\theta) \]
其中\(x\)是自变量,\(y\)是因变量,\(\theta\)是模型参数
如果自变量\(x\)只有一个,那么这种问题称为单变量线性回归(或称为一元线性回归);如果自变量\(x\)表示多个,那么成为多变量线性回归(或称为多元线性回归)
单变量线性回归
单变量线性问题可转换为求解二维平面上的直线问题
模型计算公式如下:
\[ y=w_{1}x+w_{0} \]
参数集合\(\theta = \left \{ w_{0},w_{1} \right \}\)
在学习过程中,需要判断参数\(w_{0}\)和\(w_{1}\)是否满足要求,即是否和所有数据点接近。使用均方误差(mean square error,简称MSE)来评估预测值和实际数据点的接近程度,模型评估公式如下:
\[ J(w_{0},w_{1})=\frac{1}{N}\sum_{i=1}^{N}(h(x_{i};\theta) - y_{i})^{2} \]
其中\(y_{i}\)表示真实数据,\(h\)表示估计值,\(J\)表示损失值
多变量线性回归
多变量线性回归计算公式如下:
\[ \left\{\begin{matrix} y_{1}=w_{0}+w_{1}\cdot x_{11}+...+w_{n}\cdot x_{1n}\\ y_{2}=w_{0}+w_{1}\cdot x_{21}+...+w_{n}\cdot x_{2n}\\ ...\\ y_{m}=w_{0}+w_{1}\cdot x_{m1}+...+w_{n}\cdot x_{mn} \end{matrix}\right. \]
参数\(m\)表示有\(m\)个等式,参数\(n\)表示每一组变量有\(n\)个参数。设\(x_{0}=1\),计算公式如下:
\[ \left\{\begin{matrix} y_{1}=w_{0}\cdot x_{10}+w_{1}\cdot x_{11}+...+w_{n}\cdot x_{1n}\\ y_{2}=w_{0}\cdot x_{20}+w_{1}\cdot x_{21}+...+w_{n}\cdot x_{2n}\\ ...\\ y_{m}=w_{0}\cdot x_{m0}+w_{1}\cdot x_{m1}+...+w_{n}\cdot x_{mn} \end{matrix}\right. \]
此时每组参数个数增加为\(n+1\),其向量化公式如下:
\[ Y=X\cdot W \]
其中
\[ Y_{m\times 1}=\begin{bmatrix} y_{1}\\ y_{2}\\ ...\\ y_{m} \end{bmatrix} \]
\[ X_{m\times (n+1)}=\begin{bmatrix} x_{10} & x_{11} & ... & x_{1n}\\ x_{20} & x_{21} & ... & x_{2n}\\ ... & ... & ... & ...\\ x_{m0} & x_{m1} & ... & x_{mn} \end{bmatrix} =\begin{bmatrix} 1 & x_{11} & ... & x_{1n}\\ 1 & x_{21} & ... & x_{2n}\\ ... & ... & ... & ...\\ 1 & x_{m1} & ... & x_{mn} \end{bmatrix} \]
\[ W_{(n+1)\times 1}= \begin{bmatrix} w_{0} \\ w_{1} \\ ... \\ w_{n} \end{bmatrix} \]
同样使用均方误差作为损失函数
\[ J(W)=\frac{1}{N}\sum_{i=1}^{N}(h(x_{i};W) - y_{i})^{2} \]
最小二乘法
利用最小二乘法(least square method)计算线性回归问题的参数,它通过最小化误差的平方和来求取目标函数的最优值,这样进一步转换为求取损失函数\(J\)的最小值,当\(J\)得到最小值时,参数偏导数一定为0
\[ loss=N*J=\sum_{i=1}^{N}(h(x_{i}:\theta) - y_{i})^{2} \]
有两种方式进行最小二乘法的计算,使用几何方式计算单变量线性回归问题,使用矩阵方式计算多变量线性回归问题
几何计算
当\(J\)得到最小值时,\(w_{0}\)和\(w_{1}\)的偏导数一定为0,所以参数\(w_{0}\)和\(w_{1}\)的计算公式如下:
\[ \frac{\varphi J}{\varphi w_{0}} =\frac{\varphi }{\varphi w_{0}}\frac{1}{N} \sum_{i=1}^{N}(h(x_{i})-y_{i})^{2} =\frac{\varphi }{\varphi w_{0}}\frac{1}{N} \sum_{i=1}^{N}(w_{0}+w_{1}\cdot x_{i}-y_{i})^{2} \] \[ =\frac{2}{N} \sum_{i=1}^{N}(w_{0}+w_{1}\cdot x_{i}-y_{i}) =2\cdot w_{0}+\frac{2}{N} \sum_{i=1}^{N}(w_{1}\cdot x_{i}-y_{i}) \]
\[ \frac{\varphi J}{\varphi w_{0}}=0 \Rightarrow w_{0}=-\frac{1}{N}\sum_{i=1}^{N}(w_{1}\cdot x_{i}-y_{i}) =\frac{1}{N}(\sum_{i=1}^{N}y_{i}-\sum_{i=1}^{N}w_{1}\cdot x_{i}) =\bar{y}-w_{1}\cdot \bar{x} \]
\[ \frac{\varphi J}{\varphi w_{1}} =\frac{\varphi }{\varphi w_{1}}\frac{1}{N} \sum_{i=1}^{N}(h(x_{i})-y_{i})^{2} =\frac{\varphi }{\varphi w_{1}}\frac{1}{N} \sum_{i=1}^{N}(w_{0}+w_{1}\cdot x_{i}-y_{i})^{2} \] \[ =\frac{2}{N} \sum_{i=1}^{N}(w_{0}+w_{1}\cdot x_{i}-y_{i})\cdot x_{i} =\frac{2\cdot w_{0}}{N}\sum_{i=1}^{N}x_{i}+\frac{2\cdot w_{1}}{N}\sum_{i=1}^{N}x_{i}\cdot x_{i}-\frac{2}{N}\sum_{i=1}^{N}x_{i}\cdot y_{i} \] \[ =2\cdot w_{0}\cdot \bar{x}+2\cdot w_{1}\cdot \bar{x^{2}}-2\cdot \bar{x\cdot y} \]
\[ \frac{\varphi J}{\varphi w_{1}}=0, w_{0}=\bar{y}-w_{1}\cdot \bar{x} \Rightarrow \bar{x}\cdot \bar{y}-w_{1}\cdot \bar{x}^{2}+w_{1}\cdot \bar{x^{2}}-\bar{x\cdot y}=0 \Rightarrow w_{1}=\frac{\bar{x\cdot y} - \bar{x}\cdot \bar{y}}{\bar{x^{2}}-\bar{x}^{2}} \]
最终得到的\(w_{0}\)和\(w_{1}\)的计算公式如下:
\[ w_{0}=\bar{y}-w_{1}\cdot \bar{x} \]
\[ w_{1}=\frac{\bar{x\cdot y} - \bar{x}\cdot \bar{y}}{\bar{x^{2}}-\bar{x}^{2}} \]
- 参数\(\bar{y}\)表示真实结果的均值
- 参数\(\bar{x}\)表示输入变量的均值
- 参数\(\bar{x\cdot y}\)表示输入变量和真实结果的乘积的均值
- 其他变量以此类推
矩阵计算
基本矩阵运算如下:
\[ (X\pm Y)^T = X^T\pm Y^T \]
\[ (X\cdot Y)^{T}=Y^{T}\cdot X^{T} \]
\[ (A^T)^T=A \]
\[ \left | A^{T} \right |=\left | A \right | \]
矩阵求导如下:
\[ \frac{\varphi (\theta ^{T}\cdot X)}{\varphi \theta}=X \]
\[ \frac{\varphi (X^{T}\cdot \theta )}{\varphi \theta}=X \]
\[ \frac{\varphi (\theta ^{T}\cdot \theta )}{\varphi \theta}=\theta \]
\[ \frac{\varphi (\theta ^{T}\cdot C\cdot \theta )}{\varphi \theta}=2\cdot C\cdot \theta \]
对多变量线性线性回归问题进行计算,
\[ J(W) =\frac{1}{N}\cdot \sum_{i=1}^{N}(h(x_{i};W)-y_{i})^2 =\frac{1}{N}(X\cdot W-Y)^{T}\cdot (X\cdot W -Y) \] \[ =\frac{1}{N}((X\cdot W)^T-Y^T)\cdot (X\cdot W-Y)) =\frac{1}{N}(W^T\cdot X^T-Y^T)\cdot (X\cdot W-Y)) \] \[ =\frac{1}{N}(W^T\cdot X^{T}\cdot X\cdot W-W^T\cdot X^{T}\cdot Y-Y^{T}\cdot X\cdot W+Y^{T}\cdot Y) \]
其中,\(W^T\cdot X^{T}\cdot Y\)是\(Y^{T}\cdot X\cdot W\)的转置,计算结果均为\(1\times 1\)的标量,所以大小相等,上式计算如下:
\[ J(W)=\frac{1}{N}(W^T\cdot X^{T}\cdot X\cdot W-2\cdot W^T\cdot X^{T}\cdot Y+Y^{T}\cdot Y) \]
求解\(\frac{\varphi J(W)}{\varphi W}=0\)
\[ \frac{\varphi J(W)}{\varphi W}=\frac{1}{N}\cdot X^{T}\cdot X\cdot W-\frac{1}{N}\cdot X^{T}\cdot Y=0 \]
\[ \Rightarrow X^{T}\cdot X\cdot W=X^{T}\cdot Y \]
\[ \Rightarrow W=(X^{T}\cdot X)^{-1}\cdot X^{T}\cdot Y \]
\(X^{T}\cdot X\)必须是非奇异矩阵,满足\(\left | X^{T}\cdot X \right |\neq 0\),才能保证可逆
对于矩阵的秩,有以下定理
- 对于\(n\)阶矩阵\(A\),当且仅当\(\left | A \right | \neq 0\)时,\(R(A_{n})=n\),称\(A\)为满秩矩阵
- \(R(A^T)=R(A)\)
- \(R(AB)\leq min \left \{ R(A), R(B)\right \}\)
- 设\(A\)为\(m\times n\)矩阵,则\(0\leq (A)\leq min \left \{ m,n \right \}\)
所以矩阵\(X\)的秩\(R(X)\)需要为\(n+1\)(通常样本数量\(m\)大于变量数量\(n+1\))时,才能保证能够使用最小二乘法的矩阵方式求解线性回归问题
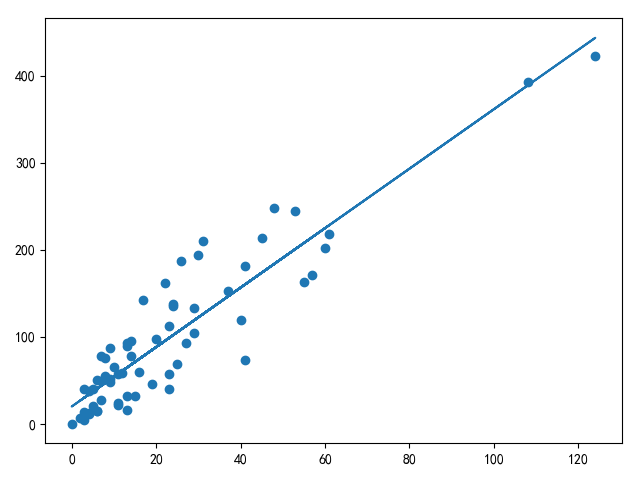
示例
单边量线性回归测试数据参考[线性回归最小二乘法和梯度下降法]的瑞典汽车保险数据集
多变量线性回归测试数据参考coursera的ex1data2.txt
1 | # -*- coding: utf-8 -*- |
适用范围
最小二乘法直接进行计算就能求出解,操作简洁,最适用于计算单变量线性回归问题
而对于多变量线性回归问题,使用最小二乘法计算需要考虑计算效率,因为\(X^T\cdot X\)的逆矩阵计算代价很大,同时需要考虑可逆问题,所以更推荐梯度下降算法来解决多变量线性回归问题
小结
本文学习了线性回归模型,利用最小二乘法(最小化误差的平方和)实现单边量/多变量线性数据的训练和预测
在训练过程中,线性回归模型使用线性映射进行前向计算,利用均方误差方法进行损失值的计算
- 对于单变量线性回归问题,适用于最小二乘法的几何计算
- 对于多变量线性回归问题,如果变量维数不大同时满足\(\left | X^{T}\cdot X \right |\neq 0\)且\(R(X) = n+1\)的情况,使用最小二乘法的矩阵计算;否则,利用梯度下降方式进行权重更新
线性回归模型更适用于回归问题,可以使用逻辑回归模型进行分类