神经网络实现-numpy

发表于 更新于 分类于
本文字数： 24k 阅读时长 ≈ 44 分钟

使用numpy实现神经网络模型

  • 使用单层神经网络OneNet实现逻辑或、逻辑与和逻辑非分类
  • 使用2层神经网络TwoNet实现逻辑异或分类
  • 使用3层神经网络ThreeNet实现iris数据集和mnist数据集分类

使用单层神经网络OneNet实现逻辑或、逻辑与和逻辑非分类

使用单层神经网络OneNet

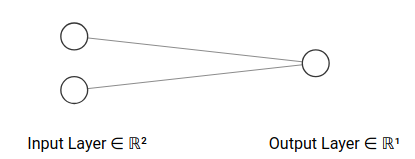
  • 输入层有2个神经元
  • 输出层有1个神经元
  • 评分函数是sigmoid
  • 损失函数是交叉熵损失

OneNet就是逻辑回归模型

  • \(L=1\)
  • \(a^{(0)}\in R^{m\times 2}\)
  • \(W^{(1)}\in R^{2\times 1}\)
  • \(b^{(1)}\in R^{1\times 2}\)
  • \(y\in R^{m\times 1}\)，每行数值表示正确类别（0或者1）

前向传播过程

\[ z^{(1)}=a^{(0)}\cdot W^{(1)} +b^{(1)} \\ h(z^{(1)})=p(y=1)=sigmoid(z^{(1)})=\frac {1}{1+e^{-z^{(1)}}} \\ \]

所以分类概率是

\[ probs=[p(y=0), p(y=1)]=[1-h(z^{(1)}), h(z^{(1)})]\\ =[\frac {e^{-z^{(1)}}}{1+e^{-z^{(1)}}}， \frac {1}{1+e^{-z^{(1)}}}] \in R^{m\times 2} \]

损失值是

\[ J(z^{(1)})=-\frac {1}{m} 1^{T}\cdot (y* \ln h(z^{(1)})+(1-y)* \ln (1-h(z^{(1)}))) \]

因为OneNet很特殊（类别不是0就是1），所以损失值可以用下式计算

\[ J(z^{(1)})=-\frac {1}{m} (y\cdot \ln h(z^{(1)})+(1-y)\cdot \ln (1-h(z^{(1)}))) \]

反向传播过程

计算最终残差\(\delta^{(L)}\)

\[ dJ=d(-\frac {1}{m} 1^{T}\cdot (y* \ln h(z^{(1)})+(1-y)* \ln (1-h(z^{(1)}))))\\ =d(-\frac {1}{m} 1^{T}\cdot (y* \ln h(z^{(1)})))+d(-\frac {1}{m} 1^{T}\cdot (1-y)* \ln (1-h(z^{(1)}))) \]

因为

\[ d(-\frac {1}{m} 1^{T}\cdot (y* \ln h(z^{(1)})))= d(-\frac {1}{m} 1^{T}\cdot (y* (h(z^{(1)})^{-1}\cdot dh(z^{(1)})))\\ =d(-\frac {1}{m} 1^{T}\cdot (y* (h(z^{(1)})^{-1}\cdot h(z^{(1)})\cdot (1-h(z^{(1)})* dz^{(1)}))))\\ =d(-\frac {1}{m} 1^{T}\cdot (y* ((1-h(z^{(1)})* dz^{(1)}))))\\ =d(-\frac {1}{m} y^{T}\cdot ((1-h(z^{(1)})* dz^{(1)})))\\ =d(-\frac {1}{m} y^{T} * (1-h(z^{(1)})^{T}\cdot dz^{(1)})) \]

\[ d(-\frac {1}{m} 1^{T}\cdot (1-y)* \ln (1-h(z^{(1)})))=d(-\frac {1}{m} 1^{T}\cdot (1-y)* ((1-h(z^{(1)}))^{-1}\cdot d(1-h(z^{(1)}))))\\ =d(-\frac {1}{m} 1^{T}\cdot (1-y)* ((1-h(z^{(1)}))^{-1}\cdot (-1)\cdot (1-h(z^{(1)}))\cdot h(z^{(1)})* dz^{(1)}))\\ =d(-\frac {1}{m} 1^{T}\cdot (1-y)* ((-1)\cdot h(z^{(1)})* dz^{(1)}))\\ =d(\frac {1}{m} 1^{T}\cdot (1-y)* (h(z^{(1)})* dz^{(1)}))\\ =d(\frac {1}{m} (1-y)^{T}\cdot (h(z^{(1)})* dz^{(1)}))\\ =d(\frac {1}{m} (1-y)^{T}* h(z^{(1)})^{T}\cdot dz^{(1)}) \]

所以

\[ dJ=d(-\frac {1}{m} y^{T} * (1-h(z^{(1)})^{T}\cdot dz^{(1)}))+ d(\frac {1}{m} (1-y)^{T}* h(z^{(1)})^{T}\cdot dz^{(1)})\\ =d(\frac {1}{m} ((1-y)^{T}* h(z^{(1)})^{T} - y^{T} * (1-h(z^{(1)})^{T})\cdot dz^{(1)}))\\ =d(\frac {1}{m} (h(z^{(1)})^{T}-y^{T}* h(z^{(1)})^{T} - y^{T} + y^{T}* h(z^{(1)})^{T})\cdot dz^{(1)}))\\ =d(\frac {1}{m} (h(z^{(1)})^{T}- y^{T})\cdot dz^{(1)})) \]

\[ D_{z^{(1)}}f(z^{(1)})=\frac {1}{m}\cdot (h(z^{(1)})^{T}- y^{T})\\ \bigtriangledown_{z^{(1)}}f(z^{(1)})=\frac {1}{m}\cdot (h(z^{(1)})- y) \]

因为OneNet是单层神经网络，所以仅有一个权重矩阵和偏置值

\[ z^{(1)}=a^{(0)}\cdot W^{(1)} +b^{(1)}\\ dz^{(1)}=a^{(0)}\cdot dW^{(1)} + db^{(1)}\\ dJ=d(\frac {1}{m} (h(z^{(1)})^{T}- y^{T})\cdot dz^{(1)}))\\ =d(\frac {1}{m} (h(z^{(1)})^{T}- y^{T})\cdot (a^{(0)}\cdot dW^{(1)} + db^{(1)})))\\ =d(\frac {1}{m} (h(z^{(1)})^{T}- y^{T})\cdot a^{(0)}\cdot dW^{(1)})+d(\frac {1}{m} (h(z^{(1)})^{T}- y^{T})\cdot db^{(1)})\\ \]

\[ D_{W^{(1)}}f(W^{(1)})=\frac {1}{m}\cdot (h(z^{(1)})^{T}- y^{T})\cdot a^{(0)}\\ \bigtriangledown_{W^{(1)}}f(W^{(1)})=\frac {1}{m}\cdot (a^{(0)})^{T}\cdot (h(z^{(1)})- y) \]

\[ D_{b^{(1)}}f(b^{(1)})=\frac {1}{m}\cdot \sum_{i=1}^{m} (h(z_{i}^{(1)})^{T}- y^{T}_{i})\\ \bigtriangledown_{b^{(1)}}f(b^{(1)})=\frac {1}{m}\cdot \sum_{i=1}^{m} (h(z_{i}^{(1)})- y_{i}) \]

偏置向量需要考虑维数

进行权重更新时添加正则化项

\[ W^{(1)} = W^{(1)} - \alpha\cdot (\nabla_{W^{(1)}} J(W, b)+\lambda \sum W^{(1)}) \]

numpy实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
# -*- coding: utf-8 -*-

# @Time    : 19-5-17 下午2:54
# @Author  : zj

import matplotlib.pyplot as plt
import numpy as np

# 批量大小
N = 4
# 输入维数
D = 2
# 输出类别
K = 1


def init_weights(inputs, outputs):
    return 0.01 * np.random.normal(loc=0.0, scale=1.0, size=(inputs, outputs))


class OneNet(object):

    def __init__(self, w, b):
        self.w = w
        self.b = b

    def forward(self, inputs):
        """
        前向计算，计算评分函数值
        """
        self.m = inputs.shape[0]
        self.a0 = inputs

        self.z1 = inputs.dot(self.w) + self.b
        self.h = self.sigmoid(self.z1)
        return self.h

    def backward(self, output):
        """
        反向传播，计算梯度
        """
        delta = (self.h - output) / self.m
        self.dw = self.a0.T.dot(delta)
        self.db = np.sum(delta, axis=0)

    def update(self, alpha=1e-3, la=1e-3):
        """
        更新梯度
        """
        self.w = self.w - alpha * (self.dw + la * np.sum(self.w))
        self.b = self.b - alpha * self.db

    def sigmoid(self, inputs):
        return 1.0 / (1 + np.exp(-1 * inputs))

    def get_parameters(self):
        return self.w, self.b


def compute_loss(score, y, beta=0.0001):
    loss = -1.0 / score.shape[0] * (y.T.dot(np.log(score + beta)) + (1 - y).T.dot(np.log(1 - score + beta)))
    return loss[0][0]


def draw(loss_list, title='损失图'):
    plt.title(title)
    plt.ylabel('损失值')
    plt.xlabel('迭代/500次')
    plt.plot(loss_list)
    plt.show()


if __name__ == '__main__':
    w = init_weights(D, K)
    b = init_weights(K, D)
    net = OneNet(w, b)

    input_array = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    or_array = np.array([[0, 0, 0, 1]]).T
    loss_list = []
    total_loss = 0
    for i in range(200000):
        score = net.forward(input_array)
        total_loss += compute_loss(score, or_array)
        net.backward(or_array)
        net.update()
        if (i % 500) == 499:
            print('epoch: %d loss: %.4f' % (i + 1, total_loss / 500))
            loss_list.append(total_loss / 500)
            total_loss = 0
    w, b = net.get_parameters()
    print('weight: {}'.format(w))
    print('bias: {}'.format(b))

    print('输入  输出  预测成绩')
    score = net.forward(input_array)
    for item in zip(input_array, or_array, score):
        print(item[0], item[1][0], item[2][0])
    draw(loss_list, '逻辑与')

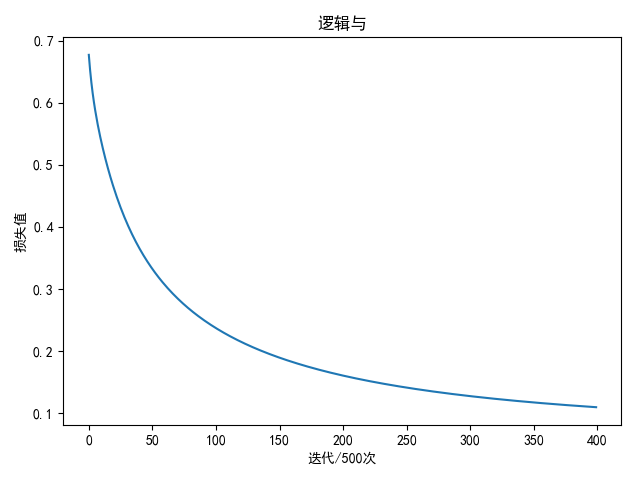
逻辑与

输入值与输出值

  • (0,0) - 0
  • (0,1) - 0
  • (1,0) - 0
  • (1,1) - 1
1
2
input_array = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
or_array = np.array([[0, 0, 0, 1]]).T

参数如下：

1
2
3
4
5
6
7
8
9
10
# 批量大小
N = 4
# 输入维数
D = 2
# 输出类别
K = 1
# 学习率
alpha=1e-3
# 正则化强度
la=1e-3

进行2万轮迭代后

1
2
3
4
5
6
7
8
weight: [[3.58627447 3.58664415]
 [3.58627445 3.58664413]]
bias: [[-5.69865399 -5.69921649]]
输入  输出  预测成绩
[0 0] 0 0.003339284003451103
[0 1] 0 0.1078994052700841
[1 0] 0 0.1078994065762308
[1 1] 1 0.8136486739472225

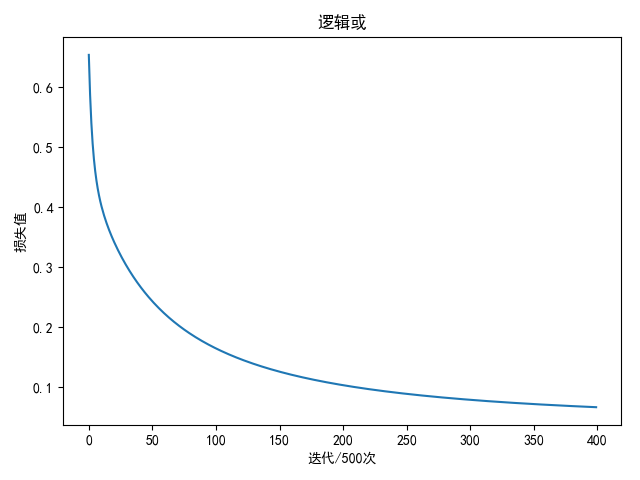
逻辑或

输入值与输出值

  • (0,0) - 0
  • (0,1) - 1
  • (1,0) - 1
  • (1,1) - 1
1
2
input_array = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
or_array = np.array([[0, 1, 1, 1]]).T

参数如下：

1
2
3
4
5
6
7
8
9
10
# 批量大小
N = 4
# 输入维数
D = 2
# 输出类别
K = 1
# 学习率
alpha=1e-3
# 正则化强度
la=1e-3

进行2万轮迭代后

1
2
3
4
5
6
7
8
weight: [[4.63629047]
 [4.63636187]]
bias: [[-1.87568775]]
输入  输出  预测成绩
[0 0] 0 0.1328849727549866
[0 1] 1 0.9405133604748699
[1 0] 1 0.9405093656227651
[1 1] 1 0.9993872646847757

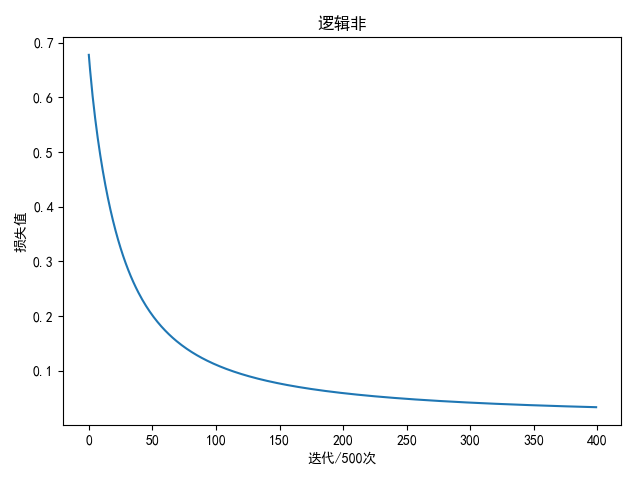
逻辑非

输入值与输出值

      • 0
      • 1
1
2
input_array = np.array([[1], [0]])
or_array = np.array([[0, 1]]).T

参数如下：

1
2
3
4
5
6
7
8
9
10
# 批量大小
N = 2
# 输入维数
D = 1
# 输出类别
K = 1
# 学习率
alpha=1e-3
# 正则化强度
la=1e-3

进行2万轮迭代后

1
2
3
4
5
weight: [[-6.79010254]]
bias: [[3.26280938]]
输入  输出  预测成绩
[1] 0 0.02854555463398659
[0] 1 0.9631306816639573

使用2层神经网络TwoNet实现逻辑异或分类

使用2层神经网络TwoNet

  • 网络层数\(L=2\)
  • 批量数据\(N\)
  • 输入层神经元个数\(D\)
  • 隐藏层神经元个数\(H\)
  • 输出层神经元个数\(K\)
  • 激活函数是relu
  • 评分函数是softmax评分
  • 损失函数是交叉熵损失平凡

  • \(a^{(0)}\in R^{N\times D}\)
  • \(W^{(1)}\in R^{D\times H}\)
  • \(b^{(1)}\in R^{1\times H}\)
  • \(W^{(2)}\in R^{H\times K}\)
  • \(b^{(2)}\in R^{1\times K}\)
  • \(Y\in R^{N\times K}\)，每行仅有正确类别为1，其余为0

前向传播过程

\[ z^{(1)}=a^{(0)}\cdot W^{(1)}+b^{(1)} \\ a^{(1)}=relu(z^{(1)}) \\ z^{(2)}=a^{(1)}\cdot W^{(2)}+b^{(2)} \]

所以分类概率是

\[ probs=h(z^{(2)})=\frac {exp(z^{(2)})}{exp(z^{(2)})\cdot A\cdot B^{T}} \]

其中\(A\in R^{K\times 1}，B\in R^{K\times 1}\)都是全\(1\)向量，

损失值是

\[ dataLoss = -\frac {1}{N} 1^{T}\cdot \ln \frac {exp(z^{(2)}* Y\cdot A)}{exp(z^{2})\cdot A} \]

\[ regLoss = 0.5\cdot reg\cdot ||W^{(1)}||^{2} + 0.5\cdot reg\cdot ||W^{(2)}||^{2} \]

\[ J(z^{(2)})=dataLoss + regLoss \]

反向传播过程

输出层输入向量梯度

\[ d(dataloss) = d(-\frac {1}{N} 1^{T}\cdot \ln \frac {exp(z^{(2)}* Y\cdot A)}{exp(z^{2})\cdot A})\\ =tr(\frac {1}{N} (probs^{T} - Y^{T})\cdot dz^{(2)}) \]

所以

\[ D_{z^{(2)}}f(z^{(2)})=\frac {1}{N} (probs^{T} - Y^{T})\\ \bigtriangledown_{z^{(2)}}f(z^{(2)})=\frac {1}{N} (probs - Y) \]

对于输出层权重矩阵、偏置向量以及隐藏层输出向量

\[ z^{(2)}=a^{(1)}\cdot W^{(2)}+b^{(2)}\\ dz^{(2)}=da^{(1)}\cdot W^{(2)} + a^{(1)}\cdot dW^{(2)} + db^{(2)} \]

\[ d(dataloss) =tr(\frac {1}{N} (probs^{T} - Y^{T})\cdot dz^{(2)})\\ =tr(\frac {1}{N} (probs^{T} - Y^{T})\cdot (da^{(1)}\cdot W^{(2)} + a^{(1)}\cdot dW^{(2)} + db^{(2)}))\\ tr(\frac {1}{N} (probs^{T} - Y^{T})\cdot da^{(1)}\cdot W^{(2)}) + tr(\frac {1}{N} (probs^{T} - Y^{T})\cdot a^{(1)}\cdot dW^{(2)}) + tr(\frac {1}{N} (probs^{T} - Y^{T})\cdot db^{(2)})) \]

输出层权重矩阵

\[ d(dataloss)=tr(\frac {1}{N} (probs^{T} - Y^{T})\cdot a^{(1)}\cdot dW^{(2)}) \]

\[ D_{W^{(2)}}f(W^{(2)})=\frac {1}{N} (probs^{T} - Y^{T})\cdot a^{(1)}\\ \bigtriangledown_{W^{(2)}}f(W^{(2)})=\frac {1}{N} (a^{(1)})^{T}\cdot (probs - Y) \]

输出层偏置向量

\[ d(dataloss)=tr(\frac {1}{N} (probs^{T} - Y^{T})\cdot db^{(2)})) \]

\[ D_{b^{(2)}}f(b^{(2)})=\frac {1}{N} \sum_{i=1}^{N}(probs_{i}^{T} - Y_{i}^{T})\\ \bigtriangledown_{b^{(2)}}f(b^{(2)})=\frac {1}{N} \sum_{i=1}^{N}(probs_{i} - Y_{i}) \]

隐藏层输出向量

\[ d(dataloss)=tr(\frac {1}{N} (probs^{T} - Y^{T})\cdot da^{(1)}\cdot W^{(2)}) =tr(\frac {1}{N} W^{(2)}\cdot (probs^{T} - Y^{T})\cdot da^{(1)}) \]

\[ D_{a^{(1)}}f(a^{(1)})=\frac {1}{N} W^{(2)}\cdot (probs^{T} - Y^{T})\\ \bigtriangledown_{a^{(1)}}f(a^{(1)})=\frac {1}{N} (probs - Y)\cdot (W^{(2)})^{T} \]

对于隐藏层输入向量

\[ a^{(1)}=relu(z^{(1)})\\ da^{(1)}=1(z^{(1)}\geq 0)* dz^{(1)} \]

\[ d(dataloss) =tr(\frac {1}{N} W^{(2)}\cdot (probs^{T} - Y^{T})\cdot da^{(1)})\\ =tr(\frac {1}{N} (W^{(2)}\cdot (probs^{T} - Y^{T}))\cdot 1(z^{(1)}\geq 0)* dz^{(1)})\\ =tr(\frac {1}{N} (W^{(2)}\cdot (probs^{T} - Y^{T}))* 1(z^{(1)}\geq 0)^{T}\cdot dz^{(1)}) \]

\[ D_{z^{(1)}}f(z^{(1)})=\frac {1}{N} (W^{(2)}\cdot (probs^{T} - Y^{T}))* 1(z^{(1)}\geq 0)^{T}\\ \bigtriangledown_{z^{(1)}}f(z^{(1)})=\frac {1}{N} ((probs - Y)\cdot (W^{(2)})^{T})* 1(z^{(1)}\geq 0) \]

对于隐藏层权重矩阵和偏置值

\[ z^{(1)}=a^{(0)}\cdot W^{(1)}+b^{(1)}\\ dz^{(1)}=da^{(0)}\cdot W^{(1)} + a^{(0)}\cdot dW^{(1)} + db^{(1)} \]

\[ d(dataloss) =tr(\frac {1}{N} (W^{(2)}\cdot (probs^{T} - Y^{T}))* 1(z^{(1)}\geq 0)^{T}\cdot dz^{(1)})\\ =tr(\frac {1}{N} (W^{(2)}\cdot (probs^{T} - Y^{T}))* 1(z^{(1)}\geq 0)^{T}\cdot (da^{(0)}\cdot W^{(1)} + a^{(0)}\cdot dW^{(1)} + db^{(1)}))\\ =tr(\frac {1}{N} (W^{(2)}\cdot (probs^{T} - Y^{T}))* 1(z^{(1)}\geq 0)^{T}\cdot (da^{(0)}\cdot W^{(1)})\\ +tr(\frac {1}{N} (W^{(2)}\cdot (probs^{T} - Y^{T}))* 1(z^{(1)}\geq 0)^{T}\cdot a^{(0)}\cdot dW^{(1)}) +tr(\frac {1}{N} (W^{(2)}\cdot (probs^{T} - Y^{T}))* 1(z^{(1)}\geq 0)^{T}\cdot db^{(1)}) \]

输出层权重矩阵

\[ d(dataloss)=tr(\frac {1}{N} (W^{(2)}\cdot (probs^{T} - Y^{T}))* 1(z^{(1)}\geq 0)^{T}\cdot a^{(0)}\cdot dW^{(1)}) \]

\[ D_{W^{(1)}}f(W^{(1)})=\frac {1}{N} (W^{(2)}\cdot (probs^{T} - Y^{T}))* 1(z^{(1)}\geq 0)^{T}\cdot a^{(0)}\\ \bigtriangledown_{W^{(1)}}f(W^{(1)})=\frac {1}{N} (a^{(0)})^{T}\cdot (W^{(2)}\cdot (probs^{T} - Y^{T}))* 1(z^{(1)}\geq 0) \]

输出层偏置向量

\[ d(dataloss)=tr(\frac {1}{N} (W^{(2)}\cdot (probs^{T} - Y^{T}))* 1(z^{(1)}\geq 0)^{T}\cdot db^{(1)}) \]

\[ D_{b^{(1)}}f(b^{(1)})=\frac {1}{N} \sum_{i=1}^{N}(W^{(2)}\cdot (probs^{T} - Y^{T}))* 1(z^{(1)}\geq 0)^{T}\\ \bigtriangledown_{b^{(1)}}f(b^{(1)})=\frac {1}{N} \sum_{i=1}^{N}((probs - Y)\cdot (W^{(2)})^{T})* 1(z^{(1)}\geq 0) \]

numpy实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
# -*- coding: utf-8 -*-

# @Time    : 19-5-17 下午6:45
# @Author  : zj

import matplotlib.pyplot as plt
import numpy as np

# 批量大小
N = 4
# 输入维数
D = 2
# 隐藏层大小
H = 30
# 输出类别
K = 2

# 学习率
learning_rate = 1e-1
# 正则化强度
lambda_rate = 1e-3


def init_weights(inputs, outputs):
    return 0.01 * np.random.normal(loc=0.0, scale=1.0, size=(inputs, outputs))


class TwoNet(object):

    def __init__(self, w, b, w2, b2):
        self.w = w
        self.b = b
        self.w2 = w2
        self.b2 = b2

    def forward(self, inputs):
        """
        前向计算，计算评分函数值
        """
        self.N = inputs.shape[0]
        self.a0 = inputs

        self.z1 = inputs.dot(self.w) + self.b
        self.a1 = np.maximum(0, self.z1)
        self.z2 = self.a1.dot(self.w2) + self.b2
        expscores = np.exp(self.z2)
        self.h = expscores / np.sum(expscores, axis=1, keepdims=True)
        return self.h

    def backward(self, output):
        """
        反向传播，计算梯度
        """
        delta = self.h
        delta[range(self.N), output] -= 1
        delta /= self.N
        self.dw2 = self.a1.T.dot(delta)
        self.db2 = np.sum(delta, axis=0, keepdims=True)

        da1 = delta.dot(self.w2.T)
        dz1 = da1
        dz1[self.z1 < 0] = 0

        self.dw = self.a0.T.dot(dz1)
        self.db = np.sum(dz1, axis=0, keepdims=True)

    def update(self):
        """
        更新梯度
        """
        self.dw2 += lambda_rate * self.w2
        self.dw += lambda_rate * self.w

        self.w2 = self.w2 - learning_rate * self.dw2
        self.b2 = self.b2 - learning_rate * self.b2

        self.w = self.w - learning_rate * self.dw
        self.b = self.b - learning_rate * self.db


def compute_loss(score, y):
    num = score.shape[0]
    data_loss = -1.0 / num * np.sum(np.log(score[range(num), y]))
    # reg_loss = 0.5 * lambda_rate * (np.sum(w ** 2) + np.sum(w2 ** 2))
    return data_loss


def compute_accuracy(y, score):
    predict = np.argmax(score, axis=1)
    return np.mean(predict == y), predict


def draw(loss_list, title='损失图'):
    plt.title(title)
    plt.ylabel('损失值')
    plt.xlabel('迭代/500次')
    plt.plot(loss_list)
    plt.show()


if __name__ == '__main__':
    w = init_weights(D, H)
    b = init_weights(1, H)
    w2 = init_weights(H, K)
    b2 = init_weights(1, K)
    net = TwoNet(w, b, w2, b2)

    input_array = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    xor_array = np.array([0, 1, 1, 0])
    loss_list = []
    total_loss = 0
    for i in range(10000):
        score = net.forward(input_array)
        total_loss += compute_loss(score, xor_array)
        net.backward(xor_array)
        net.update()
        if (i % 500) == 499:
            print('epoch: %d loss: %.4f' % (i + 1, total_loss / 500))
            loss_list.append(total_loss / 500)
            total_loss = 0
    draw(loss_list, '逻辑异或')

    w, b = net.get_parameters()
    print('weight: {}'.format(w))
    print('bias: {}'.format(b))

    score = net.forward(input_array)
    res, predict = compute_accuracy(xor_array, score)
    print('labels: ' + str(xor_array))
    print('predict: ' + str(predict))
    print('training accuracy: %.2f %%' % (res * 100))

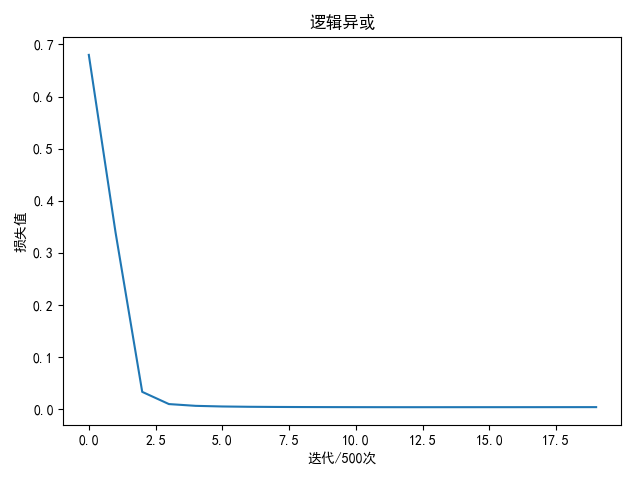
逻辑异或

输入值与输出值

  • (0,0) - 0
  • (0,1) - 1
  • (1,0) - 1
  • (1,1) - 0
1
2
input_array = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
xor_array = np.array([0, 1, 1, 0])

参数如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
# 批量大小
N = 4
# 输入维数
D = 2
# 隐藏层大小
H = 6
# 输出类别
K = 2

# 学习率
learning_rate = 1e-1
# 正则化强度
lambda_rate = 1e-3

进行1万轮迭代后

1
2
3
4
5
6
7
weight: [[-1.39091559  0.26154732 -0.90273461  1.66258303  1.63181952 -1.61815551]
 [ 1.39121663  0.26156278  0.90284832 -1.66206662  1.63189271 -1.61824032]]
bias: [[ 4.92481313e-05 -2.61570825e-01  8.55319233e-06  8.17393648e-05
  -1.63169400e+00  1.61798312e+00]]
labels: [0 1 1 0]
predict: [0 1 1 0]
training accuracy: 100.00 %

使用3层神经网络ThreeNet实现iris数据集和mnist数据集分类

使用3层神经网络ThreeNet

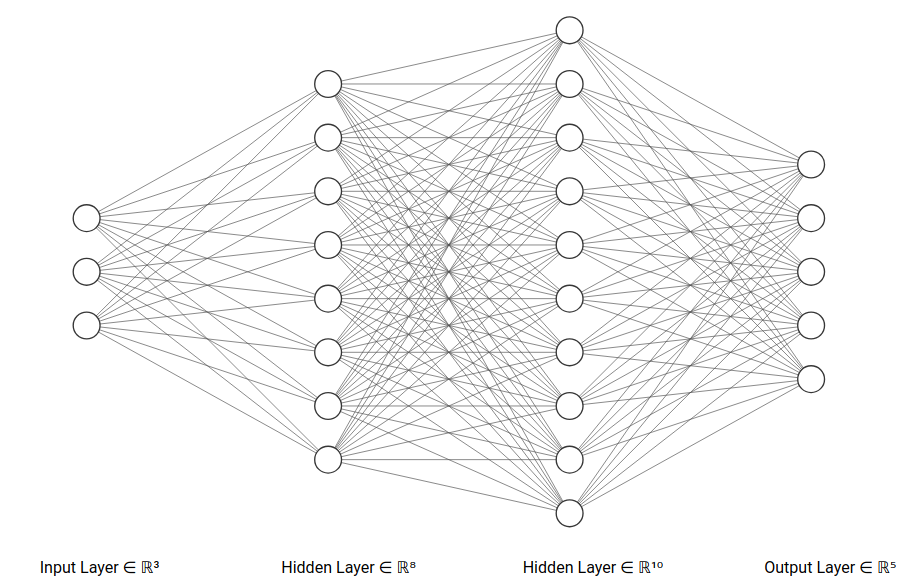
  • 网络层数\(L=3\)
  • 批量数据\(N\)
  • 输入层神经元个数\(D\)
  • 第一个隐藏层神经元个数\(H1\)
  • 第二个隐藏层神经元个数\(H2\)
  • 输出层神经元个数\(K\)
  • 激活函数是relu
  • 评分函数是softmax评分
  • 损失函数是交叉熵损失平凡

  • \(a^{(0)}\in R^{N\times D}\)
  • \(W^{(1)}\in R^{D\times H1}\)
  • \(b^{(1)}\in R^{1\times H1}\)
  • \(W^{(2)}\in R^{H1\times H2}\)
  • \(b^{(2)}\in R^{1\times H2}\)
  • \(W^{(3)}\in R^{H2\times K}\)
  • \(b^{(3)}\in R^{1\times K}\)
  • \(Y\in R^{N\times K}\)，每行仅有正确类别为1，其余为0

前向传播过程

\[ z^{(1)}=a^{(0)}\cdot W^{(1)}+b^{(1)} \\ a^{(1)}=relu(z^{(1)}) \\ z^{(2)}=a^{(1)}\cdot W^{(2)}+b^{(2)}\\ a^{(2)}=relu(z^{(2)}) \\ z^{(3)}=a^{(2)}\cdot W^{(3)}+b^{(3)}\\ \]

所以分类概率是

\[ probs=h(z^{(3)})=\frac {exp(z^{(3)})}{exp(z^{(3)})\cdot A\cdot B^{T}} \]

其中\(A\in R^{K\times 1}，B\in R^{K\times 1}\)都是全\(1\)向量，

损失值是

\[ dataLoss = -\frac {1}{N} 1^{T}\cdot \ln \frac {exp(z^{(3)}* Y\cdot A)}{exp(z^{3})\cdot A} \]

\[ regLoss = 0.5\cdot reg\cdot ||W^{(1)}||^{2} + 0.5\cdot reg\cdot ||W^{(2)}||^{2} + 0.5\cdot reg\cdot ||W^{(3)}||^{2} \]

\[ J(z^{(2)})=dataLoss + regLoss \]

反向传播过程

输出层输入向量梯度

\[ \bigtriangledown_{z^{(3)}}f(z^{(3)})=\frac {1}{N} (probs - Y) \]

对于输出层权重矩阵、偏置向量以及第二个隐藏层输出向量

\[ \bigtriangledown_{W^{(3)}}f(W^{(3)})=\frac {1}{N} (a^{(2)})^{T}\cdot (probs - Y) \]

\[ \bigtriangledown_{b^{(3)}}f(b^{(3)})=\frac {1}{N} \sum_{i=1}^{N}(probs_{i} - Y_{i}) \]

\[ \bigtriangledown_{a^{(2)}}f(a^{(2)})=\frac {1}{N} (probs - Y)\cdot (W^{(3)})^{T} \]

对于第二个隐藏层输入向量

\[ \bigtriangledown_{z^{(2)}}f(z^{(2)})=\frac {1}{N} ((probs - Y)\cdot (W^{(3)})^{T})* 1(z^{(2)}\geq 0) \]

对于第二个隐藏层权重矩阵、偏置向量和第一个隐藏层输出向量

\[ \bigtriangledown_{W^{(2)}}f(W^{(2)})=\frac {1}{N} (a^{(1)})^{T}\cdot ((W^{(3)}\cdot (probs^{T} - Y^{T}))* 1(z^{(2)}\geq 0)) \]

\[ \bigtriangledown_{b^{(2)}}f(b^{(1)})=\frac {1}{N} \sum_{i=1}^{N}((probs - Y)\cdot (W^{(3)})^{T})* 1(z^{(2)}\geq 0) \]

\[ \bigtriangledown_{a^{(1)}}f(a^{(1)})=\frac {1}{N} (((probs - Y)\cdot (W^{(3)})^{T})* 1(z^{(2)}\geq 0))\cdot (W^{(2)})^{T} \]

对于第一个隐藏层输入向量

\[ \bigtriangledown_{z^{(2)}}f(z^{(2)})=\frac {1}{N} (((probs - Y)\cdot (W^{(3)})^{T})* 1(z^{(2)}\geq 0)\cdot (W^{(2)})^{T})* 1(z^{(1)}\geq 0) \]

对于第一个隐藏层权重矩阵和偏置向量

\[ \bigtriangledown_{W^{(2)}}f(W^{(2)})=\frac {1}{N} (a^{(1)})^{T}\cdot ((((probs - Y)\cdot (W^{(3)})^{T})* 1(z^{(2)}\geq 0)\cdot (W^{(2)})^{T})* 1(z^{(1)}\geq 0)) \]

\[ \bigtriangledown_{b^{(2)}}f(b^{(1)})=\frac {1}{N} \sum_{i=1}^{N}(((probs - Y)\cdot (W^{(3)})^{T})* 1(z^{(2)}\geq 0)\cdot (W^{(2)})^{T})* 1(z^{(1)}\geq 0) \]

numpy实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
class ThreeNet(object):

    def __init__(self, w, b, w2, b2, w3, b3):
        self.w = w
        self.b = b
        self.w2 = w2
        self.b2 = b2
        self.w3 = w3
        self.b3 = b3

    def forward(self, inputs):
        """
        前向计算，计算评分函数值
        """
        self.N = inputs.shape[0]
        self.a0 = inputs

        self.z1 = inputs.dot(self.w) + self.b
        self.a1 = np.maximum(0, self.z1)

        self.z2 = self.a1.dot(self.w2) + self.b2
        self.a2 = np.maximum(0, self.z2)

        self.z3 = self.a2.dot(self.w3) + self.b3
        expscores = np.exp(self.z3)
        self.h = expscores / np.sum(expscores, axis=1, keepdims=True)
        return self.h

    def backward(self, output):
        """
        反向传播，计算梯度
        """
        delta = self.h
        delta[range(self.N), output] -= 1
        delta /= self.N

        self.dw3 = self.a2.T.dot(delta)
        self.db3 = np.sum(delta, axis=0, keepdims=True)

        da2 = delta.dot(self.w3.T)
        dz2 = da2
        dz2[self.z2 < 0] = 0

        self.dw2 = self.a1.T.dot(dz2)
        self.db2 = np.sum(dz2, axis=0, keepdims=True)

        da1 = dz2.dot(self.w2.T)
        dz1 = da1
        dz1[self.z1 < 0] = 0

        self.dw = self.a0.T.dot(dz1)
        self.db = np.sum(dz1, axis=0, keepdims=True)

    def update(self):
        """
        更新梯度
        """
        self.dw3 += lambda_rate * self.w3
        self.dw2 += lambda_rate * self.w2
        self.dw += lambda_rate * self.w

        self.w3 = self.w3 - learning_rate * self.dw3
        self.b3 = self.b3 - learning_rate * self.b3

        self.w2 = self.w2 - learning_rate * self.dw2
        self.b2 = self.b2 - learning_rate * self.b2

        self.w = self.w - learning_rate * self.dw
        self.b = self.b - learning_rate * self.db

    def __copy__(self):
        w = copy.deepcopy(self.w)
        b = copy.deepcopy(self.b)
        w2 = copy.deepcopy(self.w2)
        b2 = copy.deepcopy(self.b2)
        w3 = copy.deepcopy(self.w3)
        b3 = copy.deepcopy(self.b3)

        net = ThreeNet(w, b, w2, b2, w3, b3)
        return net

iris数据集

分类鸢尾（iris）数据集，下载地址：iris

共4个变量：

  • SepalLengthCm - 花萼长度
  • SepalWidthCm - 花萼宽度
  • PetalLengthCm - 花瓣长度
  • PetalWidthCm - 花瓣宽度

以及3个类别：

  • Iris-setosa
  • Iris-versicolor
  • Iris-virginica

网络和训练参数如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 批量大小
N = 120
# 输入维数
D = 4
# 隐藏层大小
H1 = 20
H2 = 20
# 输出类别
K = 3

# 学习率
learning_rate = 5e-2
# 正则化强度
lambda_rate = 1e-3

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
# -*- coding: utf-8 -*-

# @Time    : 19-5-18 下午2:23
# @Author  : zj

# -*- coding: utf-8 -*-

# @Time    : 19-5-18 上午11:48
# @Author  : zj

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import copy
from sklearn import utils
from sklearn.model_selection import train_test_split

# 批量大小
N = 120
# 输入维数
D = 4
# 隐藏层大小
H1 = 20
H2 = 20
# 输出类别
K = 3

# 学习率
learning_rate = 5e-2
# 正则化强度
lambda_rate = 1e-3

data_path = '../data/iris-species/Iris.csv'


def load_data(shuffle=True, tsize=0.8):
    """
    加载iris数据
    """
    data = pd.read_csv(data_path, header=0, delimiter=',')

    if shuffle:
        data = utils.shuffle(data)

    species_dict = {
        'Iris-setosa': 0,
        'Iris-versicolor': 1,
        'Iris-virginica': 2
    }
    data['Species'] = data['Species'].map(species_dict)

    data_x = np.array(
        [data['SepalLengthCm'], data['SepalWidthCm'], data['PetalLengthCm'], data['PetalWidthCm']]).T
    data_y = data['Species']

    x_train, x_test, y_train, y_test = train_test_split(data_x, data_y, train_size=tsize, test_size=(1 - tsize),
                                                        shuffle=False)

    return x_train, x_test, y_train, y_test


def init_weights(inputs, outputs):
    return 0.01 * np.random.normal(loc=0.0, scale=1.0, size=(inputs, outputs))


class ThreeNet(object):
    ...
    ...


def compute_loss(score, y):
    num = score.shape[0]
    data_loss = -1.0 / num * np.sum(np.log(score[range(num), y]))
    # reg_loss = 0.5 * lambda_rate * (np.sum(w ** 2) + np.sum(w2 ** 2))
    return data_loss


def compute_accuracy(score, y):
    predict = np.argmax(score, axis=1)
    return np.mean(predict == y)


def draw(loss_list, title='损失图', ylabel='损失值', xlabel='迭代/100次'):
    plt.title(title)
    plt.ylabel(ylabel)
    plt.xlabel(xlabel)
    plt.plot(loss_list)
    plt.show()


if __name__ == '__main__':
    x_train, x_test, y_train, y_test = load_data(shuffle=True, tsize=0.8)

    w = init_weights(D, H1)
    b = init_weights(1, H1)
    w2 = init_weights(H1, H2)
    b2 = init_weights(1, H2)
    w3 = init_weights(H2, K)
    b3 = init_weights(1, K)
    net = ThreeNet(w, b, w2, b2, w3, b3)

    loss_list = []
    total_loss = 0
    accuracy_list = []
    bestA = 0
    best_net = None
    for i in range(10000):
        score = net.forward(x_train)
        total_loss += compute_loss(score, y_train)
        net.backward(y_train)
        net.update()

        if i % 100 == 99:
            avg_loss = total_loss / 100
            print('epoch: %d loss: %.4f' % (i + 1, avg_loss))
            loss_list.append(avg_loss)
            total_loss = 0

            # 计算训练数据集检测精度
            accuracy = compute_accuracy(net.forward(x_train), y_train)
            accuracy_list.append(accuracy)
            if accuracy >= bestA:
                bestA = accuracy
                best_net = net.__copy__()

    draw(loss_list, 'iris数据集')
    draw(accuracy_list, '训练精度', '检测精度')

    test_score = best_net.forward(x_test)
    res = compute_accuracy(test_score, y_test)
    print('best train accuracy: %.2f %%' % (bestA * 100))
    print('test accuracy: %.2f %%' % (res * 100))

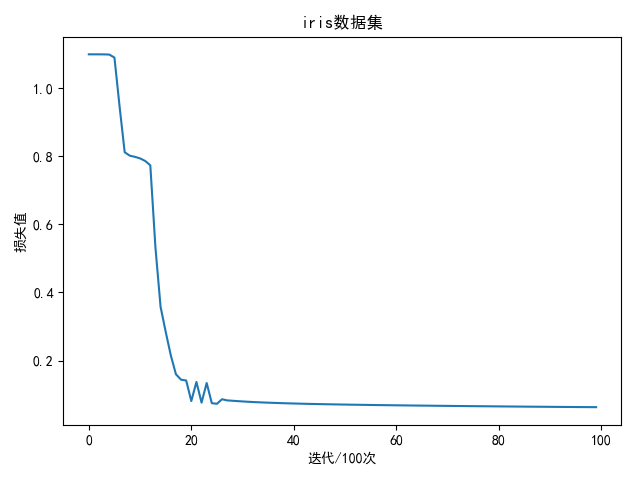
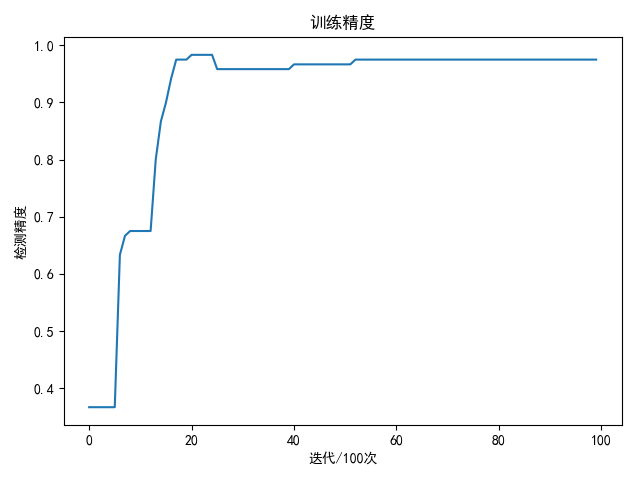
训练1万次结果如下：

1
2
best train accuracy: 98.33 %
test accuracy: 100.00 %

softmax回归神经网络
iris96.67%98.33%

mnist数据集

mnist数据集是手写数字数据集，共有共有60000张训练图像和10000张测试图像，分别表示数字0-9

数据集的下载和解压参考：Python MNIST解压

网络和训练参数如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 批量大小
batch_size = 256
# 输入维数
D = 784
# 隐藏层大小
H1 = 200
H2 = 80
# 输出类别
K = 10

# 学习率
learning_rate = 1e-3
# 正则化强度
lambda_rate = 1e-3

完整代码如下：

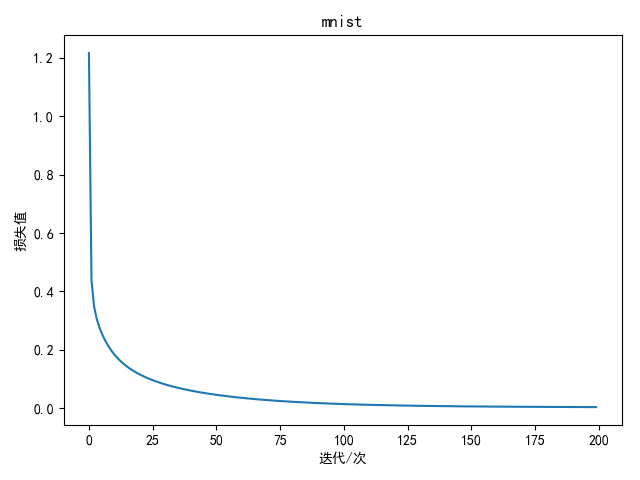
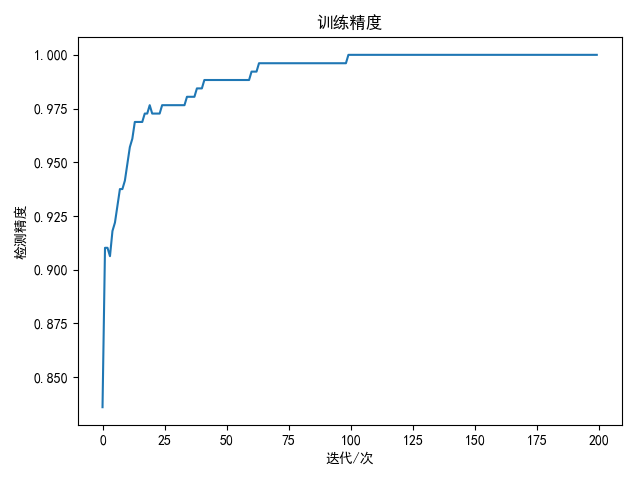
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
# -*- coding: utf-8 -*-

# @Time    : 19-5-18 上午11:48
# @Author  : zj

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import copy
import cv2
import os
import warnings

warnings.filterwarnings('ignore')

# 批量大小
batch_size = 256
# 输入维数
D = 784
# 隐藏层大小
H1 = 200
H2 = 80
# 输出类别
K = 10

# 学习率
learning_rate = 1e-3
# 正则化强度
lambda_rate = 1e-3

data_path = '../data/mnist/'

cate_list = list(range(10))


def load_data(shuffle=True):
    """
    加载mnist数据
    """
    train_dir = os.path.join(data_path, 'train')
    test_dir = os.path.join(data_path, 'test')

    x_train = []
    x_test = []
    y_train = []
    y_test = []
    train_file_list = []
    for i in cate_list:
        data_dir = os.path.join(train_dir, str(i))
        file_list = os.listdir(data_dir)
        for filename in file_list:
            file_path = os.path.join(data_dir, filename)
            train_file_list.append(file_path)

        data_dir = os.path.join(test_dir, str(i))
        file_list = os.listdir(data_dir)
        for filename in file_list:
            file_path = os.path.join(data_dir, filename)
            img = cv2.imread(file_path, cv2.IMREAD_GRAYSCALE)
            if img is not None:
                h, w = img.shape[:2]
                x_test.append(img.reshape(h * w))
                y_test.append(i)

    train_file_list = np.array(train_file_list)
    if shuffle:
        np.random.shuffle(train_file_list)

    for file_path in train_file_list:
        img = cv2.imread(file_path, cv2.IMREAD_GRAYSCALE)
        if img is not None:
            h, w = img.shape[:2]
            x_train.append(img.reshape(h * w))
            y_train.append(int(os.path.split(file_path)[0].split('/')[-1]))

    return np.array(x_train), np.array(x_test), np.array(y_train), np.array(y_test)


def init_weights(inputs, outputs):
    return 0.01 * np.random.normal(loc=0.0, scale=1.0, size=(inputs, outputs))


class ThreeNet(object):
    ...
    ...


def compute_loss(score, y):
    num = score.shape[0]
    data_loss = -1.0 / num * np.sum(np.log(score[range(num), y]))
    # reg_loss = 0.5 * lambda_rate * (np.sum(w ** 2) + np.sum(w2 ** 2))
    return data_loss


def compute_accuracy(score, y):
    predict = np.argmax(score, axis=1)
    return np.mean(predict == y)


def draw(loss_list, title='损失图', ylabel='损失值', xlabel='迭代/100次'):
    plt.title(title)
    plt.ylabel(ylabel)
    plt.xlabel(xlabel)
    plt.plot(loss_list)
    plt.show()


if __name__ == '__main__':
    x_train, x_test, y_train, y_test = load_data(shuffle=True)

    w = init_weights(D, H1)
    b = init_weights(1, H1)
    w2 = init_weights(H1, H2)
    b2 = init_weights(1, H2)
    w3 = init_weights(H2, K)
    b3 = init_weights(1, K)
    net = ThreeNet(w, b, w2, b2, w3, b3)

    loss_list = []
    total_loss = 0
    accuracy_list = []
    bestA = 0
    best_net = None
    range_list = np.arange(0, x_train.shape[0] - batch_size, step=batch_size)
    for i in range(200):
        for j in range_list:
            data = x_train[j:j + batch_size]
            labels = y_train[j:j + batch_size]

            score = net.forward(data)
            total_loss += compute_loss(score, labels)
            net.backward(labels)
            net.update()

            if j == range_list[-1]:
                avg_loss = total_loss / len(range_list)
                print('epoch: %d loss: %.4f' % (i + 1, avg_loss))
                loss_list.append(avg_loss)
                total_loss = 0

                # 计算训练数据集检测精度
                score = net.forward(x_train[j:j + batch_size])
                accuracy = compute_accuracy(score, labels)
                accuracy_list.append(accuracy)
                if accuracy >= bestA:
                    bestA = accuracy
                    best_net = net.__copy__()
                break

    draw(loss_list, title='mnist', xlabel='迭代/次')
    draw(accuracy_list, title='训练精度', ylabel='检测精度', xlabel='迭代/次')

    test_score = best_net.forward(x_test)
    res = compute_accuracy(test_score, y_test)
    print('best train accuracy: %.2f %%' % (bestA * 100))
    print('test accuracy: %.2f %%' % (res * 100))

训练200次结果如下：

1
2
best train accuracy: 100.00 %
test accuracy: 97.92 %

softmax回归神经网络
mnist92.15%97.92%

相关阅读