正态分布
正态分布(normal distribution),也称为常态分布,高斯分布(gaussian distribution),是连续随机变量概率分布的一种,自然界中大量现象符合正态分布,比如身高/体重/成绩/收入/寿命
一维正态分布
若随机变量\(X\)服从一个位置参数(数学期望)为\(\mu\)、尺度参数(方差)为$$的概率分布,且其概率密度函数为
\[ f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) \]
则这个随机变量就称为正态随机变量,正态随机变量服从的分布就称为正态分布,记作\(X \sim N\left(\mu, \sigma^{2}\right)\)
标准正态分布
当\(\mu =0, \sigma =1\)的正态分布称为标准正态分布
特性
期望值\(\mu\)决定了概率密度函数的分布位置,离\(\mu\)近的值概率大,反之概率小
正态分布以\(\mu\)为对称轴,左右完全对称;正态分布的期望、均数、中位数和总数都是\(\mu\)
方差\(\sigma\)决定了分布幅度大小(离散程度),\(\sigma\)越大,数据分布越分散,曲线越扁平;反之,数据越集中,曲线越廋高
通常称发生概率小于5%的事件几乎不可能发生,在\(\left ( \mu-3\cdot \sigma,\mu+3\cdot \sigma \right )\)区间外的概率小于千分之三,所以基本上把区间\(\left ( \mu-3\cdot \sigma,\mu+3\cdot \sigma \right )\)称为随机变量x实际可能的取值范围,称为正态分布的\(3\sigma\)原则
中心极限定理:多个独立分布的随机变量的和的均值服从正态分布
示例
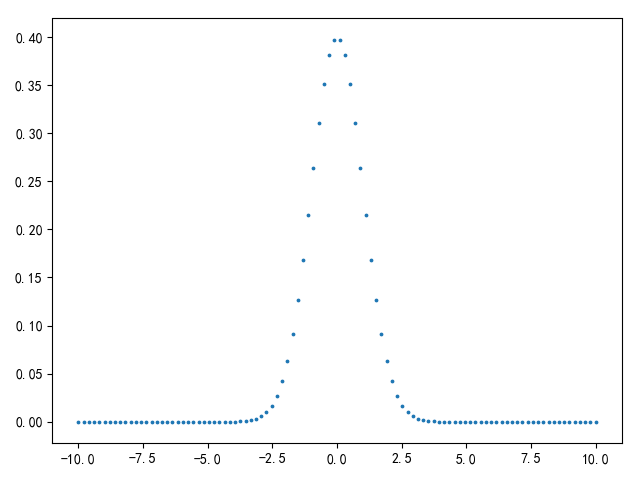
参考python pylab plot normal distribution,标准正态分布如下
1 | import matplotlib.pyplot as plt |