神经网络推导-批量数据
输入批量数据到神经网络,进行前向传播和反向传播的推导
TestNet网络
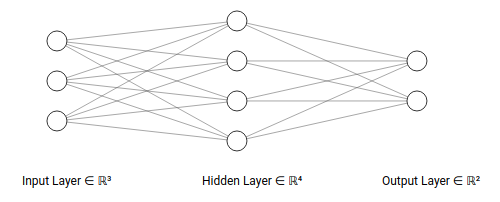
TestNet是一个2层神经网络,结构如下:
- 输入层有
3个神经元 - 隐藏层有
4个神经元 - 输出层有
2个神经元
- 激活函数为
relu函数 - 评分函数为
softmax回归 - 代价函数为交叉熵损失
网络符号定义
规范神经网络的计算符号
关于神经元和层数
- \(L\)表示网络层数(不计入输入层)
- \(L=2\),其中输入层是第
0层,隐藏层是第1层,输出层是第2层
- \(L=2\),其中输入层是第
- \(n^{(l)}\)表示第\(l\)层的神经元个数(不包括偏置神经元)
- \(n^{(0)}=3\),表示输入层神经元个数为
3 - \(n^{(1)}=4\),表示隐藏层神经元个数为
4 - \(n^{(2)}=2\),表示输出层神经元个数为
2
- \(n^{(0)}=3\),表示输入层神经元个数为
关于权重矩阵和偏置值
- \(W^{(l)}\)表示第\(l-1\)层到第\(l\)层的权重矩阵,矩阵行数为第\(l-1\)层的神经元个数,列数为第\(l\)层神经元个数
- \(W^{(1)}\)表示输入层到隐藏层的权重矩阵,大小为\(R^{3\times 4}\)
- \(W^{(2)}\)表示隐藏层到输出层的权重矩阵,大小为\(R^{4\times 2}\)
- \(W^{(l)}_{i,j}\)表示第\(l-1\)层第\(i\)个神经元到第\(l\)第\(j\)个神经元的权值
- \(i\)的取值范围是\([1,n^{(l-1)}]\)
- \(j\)的取值范围是\([1, n^{(l)}]\)
- \(W^{(l)}_{i}\)表示第\(l-1\)层第\(i\)个神经元对应的权重向量,大小为\(n^{(l)}\)
- \(W^{(l)}_{,j}\)表示第\(l\)层第\(j\)个神经元对应的权重向量,大小为\(n^{(l-1)}\)
- \(b^{(l)}\)表示第\(l\)层的偏置向量
- \(b^{(1)}\)表示输入层到隐藏层的偏置向量,大小为\(R^{1\times 4}\)
- \(b^{(2)}\)表示隐藏层到输出层的偏置向量,大小为\(R^{1\times 2}\)
- \(b^{(l)}_{i}\)表示第\(l\)层第\(i\)个神经元的偏置值
- \(b^{(1)}_{2}\)表示第\(1\)层隐藏层第\(2\)个神经元的偏置值
关于神经元输入向量和输出向量
- \(a^{(l)}\)表示第\(l\)层输出向量,\(a^{(l)}=[a^{(l)}_{1},a^{(l)}_{2},...,a^{(l)}_{m}]^{T}\)
- \(a^{(0)}\)表示输入层输出向量,大小为\(R^{m\times 3}\)
- \(a^{(1)}\)表示隐藏层输出向量,大小为\(R^{m\times 4}\)
- \(a^{(2)}\)表示输出层输出向量,大小为\(R^{m\times 2}\)
- \(a^{(l)}_{i}\)表示第\(l\)层第\(i\)个单元的输出值,其是输入向量经过激活计算后的值
- \(a^{(1)}_{3}\)表示隐含层第\(3\)个神经元的输入值,\(a^{(1)}_{3}=g(z^{(1)}_{3})\)
- \(z^{(l)}\)表示第\(l\)层输入向量,\(z^{(l)}=[z^{(l)}_{1},z^{(l)}_{2},...,z^{(l)}_{m}]^{T}\)
- \(z^{(1)}\)表示隐藏层的输入向量,大小为\(R^{m\times 4}\)
- \(z^{(2)}\)表示输出层的输入向量,大小为\(R^{m\times 2}\)
- \(z^{(l)}_{i,j}\)表示第\(l\)层第\(j\)个单元的输入值,其是上一层输出向量第\(i\)个数据和该层第\(j\)个神经元权重向量的加权累加和
- \(z^{(1)}_{1,2}\)表示隐藏层第\(2\)个神经元的输入值,\(z^{(1)}_{1,2}=b^{(2)}_{2}+a^{(0)}_{1,1}\cdot W^{(1)}_{1,2}+a^{(0)}_{1,2}\cdot W^{(1)}_{2,2}+a^{(0)}_{1,3}\cdot W^{(1)}_{3,2}\)
关于神经元激活函数
- \(g()\)表示激活函数操作
关于评分函数和损失函数
- \(h()\)表示评分函数操作
- \(J()\)表示代价函数操作
神经元执行步骤
神经元操作分为2步计算:
- 输入向量\(z^{(l)}\)=前一层神经元输出向量\(a^{(l-1)}\)与权重矩阵\(W^{(l)}\)的加权累加和+偏置向量
\[ z^{(l)}_{i,j}=a^{(l-1)}_{i}\cdot W^{(l)}_{,j} + b^{(l)}_{j} \Rightarrow z^{(l)}=a^{(l-1)}\cdot W^{(l)} + b^{(l)} \]
- 输出向量\(a^{(l)}\)=对输入向量\(z^{(l)}\)进行激活函数操作
\[ a^{(l)}_{i}=g(z_{i}^{(l)}) \Rightarrow a^{(l)}=g(z^{(l)}) \]
网络结构
对输入层
\[ a^{(0)} =\begin{bmatrix} a^{(0)}_{1}\\ \vdots\\ a^{(0)}_{m} \end{bmatrix} =\begin{bmatrix} a^{(0)}_{1,1} & a^{(0)}_{1,2} & a^{(0)}_{1,3}\\ \vdots & \vdots & \vdots\\ a^{(0)}_{m,1} & a^{(0)}_{m,2} & a^{(0)}_{m,3} \end{bmatrix}\in R^{m\times 3} \]
对隐藏层
\[ W^{(1)} =\begin{bmatrix} W^{(1)}_{1,1} & W^{(1)}_{1,2} & W^{(1)}_{1,3} & W^{(1)}_{1,4}\\ W^{(1)}_{2,1} & W^{(1)}_{2,2} & W^{(1)}_{2,3} & W^{(1)}_{2,4}\\ W^{(1)}_{3,1} & W^{(1)}_{3,2} & W^{(1)}_{3,3} & W^{(1)}_{3,4} \end{bmatrix} \in R^{3\times 4} \]
\[ b^{(1)}=[[b^{(1)}_{1},b^{(1)}_{2},b^{(1)}_{3},b^{(1)}_{4}]]\in R^{1\times 4} \]
\[ z^{(1)} =\begin{bmatrix} z^{(0)}_{1,1} & z^{(0)}_{1,2} & z^{(0)}_{1,3} & z^{(0)}_{1,4}\\ \vdots & \vdots & \vdots & \vdots\\ z^{(0)}_{m,1} & z^{(0)}_{m,2} & z^{(0)}_{m,3} & z^{(0)}_{m,4} \end{bmatrix}\in R^{m\times 4} \]
\[ a^{(1)} =\begin{bmatrix} a^{(0)}_{1,1} & a^{(0)}_{1,2} & a^{(0)}_{1,3} & a^{(0)}_{1,4}\\ \vdots & \vdots & \vdots & \vdots\\ a^{(0)}_{m,1} & a^{(0)}_{m,2} & a^{(0)}_{m,3} & a^{(0)}_{m,4} \end{bmatrix}\in R^{m\times 4} \]
对输出层
\[ W^{(2)} =\begin{bmatrix} W^{(2)}_{1,1} & W^{(2)}_{1,2}\\ W^{(2)}_{2,1} & W^{(2)}_{2,2}\\ W^{(2)}_{3,1} & W^{(2)}_{3,2}\\ W^{(2)}_{4,1} & W^{(2)}_{4,2} \end{bmatrix} \in R^{4\times 2} \]
\[ b^{(2)}=[[b^{(2)}_{1},b^{(2)}_{2}]]\in R^{1\times 2} \]
\[ z^{(2)} =\begin{bmatrix} z^{(2)}_{1,1} & z^{(0)}_{1,2}\\ \vdots & \vdots\\ z^{(2)}_{m,1} & z^{(0)}_{m,2} \end{bmatrix}\in R^{m\times 2} \]
评分值
\[ h(z^{(2)}) =\begin{bmatrix} p(y_{1}=1) & p(y_{1}=2)\\ \vdots & \vdots\\ p(y_{m}=1) & p(y_{m}=2) \end{bmatrix}\in R^{m\times 2} \]
损失值
\[ J(z^{(2)})=(-1)\sum_{i=1}^{m} \sum_{j=1}^{2}\cdot 1(y_{m,j}=1)\ln p(y_{m,j}=1)\in R^{1} \]
前向传播
输入层到隐藏层计算
\[ z^{(1)}_{i,1}=a^{(0)}_{i}\cdot W^{(1)}_{,1}+b^{(1)}_{1} =a^{(0)}_{i,1}\cdot W^{(1)}_{1,1} +a^{(0)}_{i,2}\cdot W^{(1)}_{2,1} +a^{(0)}_{i,3}\cdot W^{(1)}_{3,1} +b^{(1)}_{1,1} \]
\[ z^{(1)}_{i,2}=a^{(0)}_{i}\cdot W^{(1)}_{,2}+b^{(1)}_{2} =a^{(0)}_{i,1}\cdot W^{(1)}_{1,2} +a^{(0)}_{i,2}\cdot W^{(1)}_{2,2} +a^{(0)}_{i,3}\cdot W^{(1)}_{3,2} +b^{(1)}_{1,2} \]
\[ z^{(1)}_{i,3}=a^{(0)}_{i}\cdot W^{(1)}_{,3}+b^{(1)}_{3} =a^{(0)}_{i,1}\cdot W^{(1)}_{1,3} +a^{(0)}_{i,2}\cdot W^{(1)}_{2,3} +a^{(0)}_{i,3}\cdot W^{(1)}_{3,3} +b^{(1)}_{1,3} \]
\[ z^{(1)}_{i,4}=a^{(0)}_{i}\cdot W^{(1)}_{,4}+b^{(1)}_{4} =a^{(0)}_{i,1}\cdot W^{(1)}_{1,4} +a^{(0)}_{i,2}\cdot W^{(1)}_{2,4} +a^{(0)}_{i,3}\cdot W^{(1)}_{3,4} +b^{(1)}_{1,4} \]
\[ \Rightarrow z^{(1)}_{i} =[z^{(1)}_{i,1},z^{(1)}_{i,2},z^{(1)}_{i,3},z^{(1)}_{i,4}] =a^{(0)}_{i}\cdot W^{(1)}+b^{(1)} \]
\[ \Rightarrow z^{(1)} =a^{(0)}\cdot W^{(1)}+b^{(1)} \]
隐藏层输入向量到输出向量
\[ a^{(1)}_{i,1}=relu(z^{(1)}_{i,1}) \\ a^{(1)}_{i,2}=relu(z^{(1)}_{i,2}) \\ a^{(1)}_{i,3}=relu(z^{(1)}_{i,3}) \\ a^{(1)}_{i,4}=relu(z^{(1)}_{i,4}) \]
\[ \Rightarrow a^{(1)}_{i}=[a^{(1)}_{i,1},a^{(1)}_{i,2},a^{(1)}_{i,3},a^{(1)}_{i,4}] =relu(z^{(1)}_{i}) \]
\[ \Rightarrow a^{(1)}=relu(z^{(1)}) \]
隐藏层到输出层计算
\[ z^{(2)}_{i,1}=a^{(1)}_{i}\cdot W^{(2)}_{,1}+b^{(2)}_{1,1} =a^{(1)}_{i,1}\cdot W^{(2)}_{1,1} +a^{(1)}_{i,2}\cdot W^{(2)}_{2,1} +a^{(1)}_{i,3}\cdot W^{(2)}_{3,1} +a^{(1)}_{i,4}\cdot W^{(2)}_{4,1} +b^{(2)}_{1,1} \]
\[ z^{(2)}_{i,2}=a^{(1)}_{i}\cdot W^{(2)}_{,2}+b^{(2)}_{1,2} =a^{(1)}_{i,1}\cdot W^{(2)}_{1,2} +a^{(1)}_{i,2}\cdot W^{(2)}_{2,2} +a^{(1)}_{i,3}\cdot W^{(2)}_{3,2} +a^{(1)}_{i,4}\cdot W^{(2)}_{4,2} +b^{(2)}_{1,2} \]
\[ \Rightarrow z^{(2)}_{i} =[z^{(2)}_{i,1},z^{(2)}_{i,2}] =a^{(1)}_{i}\cdot W^{(2)}+b^{(2)} \]
\[ \Rightarrow z^{(2)} =a^{(1)}\cdot W^{(2)}+b^{(2)} \]
评分操作
\[ p(y_{i}=1)=\frac {exp(z^{(2)}_{i,1})}{\sum exp(z^{(2)}_{i})} \\ p(y_{i}=2)=\frac {exp(z^{(2)}_{i,2})}{\sum exp(z^{(2)}_{i})} \]
\[ \Rightarrow h(z^{(2)}_{i}) =[p(y_{i}=1),p(y_{i}=2)] =[\frac {exp(z^{(2)}_{i,1})}{\sum exp(z^{(2)}_{i})}, \frac {exp(z^{(2)}_{i,2})}{\sum exp(z^{(2)}_{i})}] \]
\[ \Rightarrow h(z^{(2)}) =\begin{bmatrix} p(y_{1}=1) & p(y_{1}=2) \\ \vdots & \vdots\\ p(y_{m}=1) & p(y_{m}=2) \end{bmatrix} \]
损失值
\[ J(z^{(2)})=(-1)\sum_{i=1}^{m} \sum_{j=1}^{2}\cdot 1(y_{m,j}=1)\ln p(y_{m,j}=1) \]
反向传播
计算输出层输入向量梯度
\[ \frac {\partial J}{\partial z^{(2)}_{i,1}}= (-1)\cdot \frac {1(y_{i}=1)}{p(y_{i}=1)}\cdot \frac {\partial p(y_{i}=1)}{\partial z^{(2)}_{i,1}} +(-1)\cdot \frac {1(y_{i}=2)}{p(y_{i}=2)}\cdot \frac {\partial p(y_{i}=2)}{\partial z^{(2)}_{i,1}} \]
\[ \frac {\partial p(y_{i}=1)}{\partial z^{(2)}_{i,1}} =\frac {exp(z^{(2)}_{i,1})\cdot \sum exp(z^{(2)}_{i})-exp(z^{(2)}_{i,1})\cdot exp(z^{(2)}_{i,1})}{(\sum exp(z^{(2)}_{i}))^2} =\frac {exp(z^{(2)}_{i,1})}{\sum exp(z^{(2)}_{i})} -(\frac {exp(z^{(2)}_{i,1})}{\sum exp(z^{(2)}_{i})})^2 =p(y_{i}=1)-(p(y_{i}=1))^2 \]
\[ \frac {\partial p(y_{i}=2)}{\partial z^{(2)}_{i,1}} =\frac {-exp(z^{(2)}_{i,2})\cdot exp(z^{(2)}_{i,1})}{(\sum exp(z^{(2)}_{i}))^2} =(-1)\cdot \frac {exp(z^{(2)}_{i,1})}{\sum exp(z^{(2)}_{i})}\cdot \frac {exp(z^{(2)}_{i,2})}{\sum exp(z^{(2)}_{i})} =(-1)\cdot p(y_{i}=1)p(y_{i}=2) \]
\[ \Rightarrow \frac {\partial J}{\partial z^{(2)}_{i,1}} =(-1)\cdot \frac {1(y_{i}=1)}{p(y_{i}=1)}\cdot (p(y_{i}=1)-(p(y_{i}=1))^2) +(-1)\cdot \frac {1(y_{i}=2)}{p(y_{i}=2)}\cdot (-1)\cdot p(y_{i}=1)p(y_{i}=2) \\ =(-1)\cdot 1(y_{i}=1)\cdot (1-p(y_{i}=1)) +1(y_{i}=2)\cdot p(y_{i}=1) =p(y_{i}=1)-1(y_{i}=1) \]
\[ \Rightarrow \frac {\partial J}{\partial z^{(2)}_{i,2}} =p(y_{i}=2)-1(y_{i}=2) \]
\[ \Rightarrow \frac {\partial J}{\partial z^{(2)}_{i}} =[p(y_{i}=1)-1(y_{i}=1), p(y_{i}=2)-1(y_{i}=2)] \]
\[ \Rightarrow \frac {\partial J}{\partial z^{(2)}} =\begin{bmatrix} p(y_{1}=1)-1(y_{1}=1) & p(y_{1}=2)-1(y_{1}=2)\\ \vdots & \vdots\\ p(y_{m}=1)-1(y_{m}=1) & p(y_{m}=2)-1(y_{m}=2) \end{bmatrix} \]
计算输出层权重向量梯度
\[ \frac {\partial J}{\partial W^{(2)}_{1,1}} =\frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(2)}_{i,1}}\cdot \frac {\partial z^{(2)}_{i,1}}{\partial W^{(2)}_{1,1}} =\frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=1)-1(y_{i}=1))\cdot a^{(1)}_{i,1}) \]
\[ \frac {\partial J}{\partial W^{(2)}_{2,1}} =\frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(2)}_{i,1}}\cdot \frac {\partial z^{(2)}_{i,1}}{\partial W^{(2)}_{2,1}} =\frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=1)-1(y_{i}=1))\cdot a^{(1)}_{i,2}) \]
\[ \frac {\partial J}{\partial W^{(2)}_{3,1}} =\frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(2)}_{i,1}}\cdot \frac {\partial z^{(2)}_{i,1}}{\partial W^{(2)}_{3,1}} =\frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=1)-1(y_{i}=1))\cdot a^{(1)}_{i,3}) \]
\[ \frac {\partial J}{\partial W^{(2)}_{4,1}} =\frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(2)}_{i,1}}\cdot \frac {\partial z^{(2)}_{i,1}}{\partial W^{(2)}_{4,1}} =\frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=1)-1(y_{i}=1))\cdot a^{(1)}_{i,4}) \]
\[ \frac {\partial J}{\partial W^{(2)}_{1,2}} =\frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(2)}_{i,2}}\cdot \frac {\partial z^{(2)}_{2}}{\partial W^{(2)}_{1,2}} =\frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=2)-1(y_{i}=2))\cdot a^{(1)}_{i,1}) \]
\[ \frac {\partial J}{\partial W^{(2)}_{2,2}} =\frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(2)}_{i,2}}\cdot \frac {\partial z^{(2)}_{2}}{\partial W^{(2)}_{2,2}} =\frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=2)-1(y_{i}=2))\cdot a^{(1)}_{i,2}) \]
\[ \frac {\partial J}{\partial W^{(2)}_{3,2}} =\frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(2)}_{i,2}}\cdot \frac {\partial z^{(2)}_{2}}{\partial W^{(2)}_{3,2}} =\frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=2)-1(y_{i}=2))\cdot a^{(1)}_{i,3}) \]
\[ \frac {\partial J}{\partial W^{(2)}_{4,2}} =\frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(2)}_{i,2}}\cdot \frac {\partial z^{(2)}_{2}}{\partial W^{(2)}_{4,2}} =\frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=2)-1(y_{i}=2))\cdot a^{(1)}_{i,4}) \]
\[ \Rightarrow \frac {\partial J}{\partial W^{(2)}} =\begin{bmatrix} \frac {\partial J}{\partial W^{(2)}_{1,1}} & \frac {\partial J}{\partial W^{(2)}_{1,2}}\\ \frac {\partial J}{\partial W^{(2)}_{2,1}} & \frac {\partial J}{\partial W^{(2)}_{2,2}}\\ \frac {\partial J}{\partial W^{(2)}_{3,1}} & \frac {\partial J}{\partial W^{(2)}_{3,2}}\\ \frac {\partial J}{\partial W^{(2)}_{4,1}} & \frac {\partial J}{\partial W^{(2)}_{4,2}} \end{bmatrix} \]
\[ =\begin{bmatrix} \frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=1)-1(y_{i}=1))\cdot a^{(1)}_{i,1}) & \frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=1)-1(y_{i}=1))\cdot a^{(1)}_{i,2})\\ \frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=1)-1(y_{i}=1))\cdot a^{(1)}_{i,3}) & \frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=1)-1(y_{i}=1))\cdot a^{(1)}_{i,4})\\ \frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=2)-1(y_{i}=2))\cdot a^{(1)}_{i,1}) & \frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=2)-1(y_{i}=2))\cdot a^{(1)}_{i,2})\\ \frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=2)-1(y_{i}=2))\cdot a^{(1)}_{i,3}) & \frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=2)-1(y_{i}=2))\cdot a^{(1)}_{i,4}) \end{bmatrix} \]
\[ =\frac {1}{m}\sum_{i=1}^{m} \begin{bmatrix} a^{(1)}_{i,1}\\ a^{(1)}_{i,2}\\ a^{(1)}_{i,3}\\ a^{(1)}_{i,4} \end{bmatrix} \begin{bmatrix} p(y_{i}=1)-1(y_{i}=1) & p(y_{i}=2)-1(y_{i}=2) \end{bmatrix}\\ =\frac {1}{m}\sum_{i=1}^{m} ((a^{(1)}_{i})^{T}\cdot \frac {\partial J}{\partial z^{(2)}_{i}}) =\frac {1}{m} (a^{(1)})^{T}\cdot \frac {\partial J}{\partial z^{(2)}} =\frac {1}{m}\sum_{i=1}^{m} (R^{4\times m}\cdot R^{m\times 2}) =R^{4\times 2} \]
计算隐藏层输出向量梯度
\[ \frac {\partial J}{\partial a^{(1)}_{i,1}} =\frac {\partial J}{\partial z^{(2)}_{i,1}}\cdot \frac {\partial z^{(2)}_{i,1}}{\partial a^{(1)}_{i,1}} +\frac {\partial J}{\partial z^{(2)}_{i,2}}\cdot \frac {\partial z^{(2)}_{i,2}}{\partial a^{(1)}_{i,1}} =(p(y_{i}=1)-1(y_{i}=1))\cdot W^{(2)}_{1,1} +(p(y_{i}=2)-1(y_{i}=2))\cdot W^{(2)}_{1,2} \]
\[ \frac {\partial J}{\partial a^{(1)}_{i,2}} =\frac {\partial J}{\partial z^{(2)}_{i,1}}\cdot \frac {\partial z^{(2)}_{i,1}}{\partial a^{(1)}_{i,2}} +\frac {\partial J}{\partial z^{(2)}_{i,2}}\cdot \frac {\partial z^{(2)}_{i,2}}{\partial a^{(1)}_{i,2}} =(p(y_{i}=1)-1(y_{i}=1))\cdot W^{(2)}_{2,1} +(p(y_{i}=2)-1(y_{i}=2))\cdot W^{(2)}_{2,2} \]
\[ \frac {\partial J}{\partial a^{(1)}_{i,3}} =\frac {\partial J}{\partial z^{(2)}_{i,1}}\cdot \frac {\partial z^{(2)}_{i,1}}{\partial a^{(1)}_{i,3}} +\frac {\partial J}{\partial z^{(2)}_{i,2}}\cdot \frac {\partial z^{(2)}_{i,2}}{\partial a^{(1)}_{i,3}} =(p(y_{i}=1)-1(y_{i}=1))\cdot W^{(2)}_{3,1} +(p(y_{i}=2)-1(y_{i}=2))\cdot W^{(2)}_{3,2} \]
\[ \frac {\partial J}{\partial a^{(1)}_{i,4}} =\frac {\partial J}{\partial z^{(2)}_{i,1}}\cdot \frac {\partial z^{(2)}_{i,1}}{\partial a^{(1)}_{i,4}} +\frac {\partial J}{\partial z^{(2)}_{i,2}}\cdot \frac {\partial z^{(2)}_{i,2}}{\partial a^{(1)}_{i,4}} =(p(y_{i}=1)-1(y_{i}=1))\cdot W^{(2)}_{4,1} +(p(y_{i}=2)-1(y_{i}=2))\cdot W^{(2)}_{4,2} \]
\[ \Rightarrow \frac {\partial J}{\partial a^{(1)}_{i}} =\begin{bmatrix} p(y_{i}=1)-1(y_{i}=1) & p(y_{i}=2)-1(y_{i}=2) \end{bmatrix} \begin{bmatrix} W^{(2)}_{1,1} & W^{(2)}_{2,1} & W^{(2)}_{3,1} & W^{(2)}_{4,1}\\ W^{(2)}_{1,2} & W^{(2)}_{2,2} & W^{(2)}_{3,2} & W^{(2)}_{4,2} \end{bmatrix} \\ =\frac {\partial J}{\partial z^{(2)}_{i}}\cdot (W^{(2)})^T =R^{1\times 2}\cdot R^{2\times 4} =R^{1\times 4} \]
\[ \Rightarrow \frac {\partial J}{\partial a^{(1)}} =\begin{bmatrix} p(y_{1}=1)-1(y_{1}=1) & p(y_{1}=2)-1(y_{1}=2)\\ \vdots & \vdots\\ p(y_{m}=1)-1(y_{m}=1) & p(y_{m}=2)-1(y_{m}=2) \end{bmatrix} \begin{bmatrix} W^{(2)}_{1,1} & W^{(2)}_{2,1} & W^{(2)}_{3,1} & W^{(2)}_{4,1}\\ W^{(2)}_{1,2} & W^{(2)}_{2,2} & W^{(2)}_{3,2} & W^{(2)}_{4,2} \end{bmatrix} \\ =\frac {\partial J}{\partial z^{(2)}}\cdot (W^{(2)})^T =R^{m\times 2}\cdot R^{2\times 4} =R^{m\times 4} \]
计算隐藏层输入向量的梯度
\[ \frac {\partial J}{\partial z^{(1)}_{i,1}} =\frac {\partial J}{\partial a^{(1)}_{i,1}}\cdot \frac {\partial a^{(1)}_{i,1}}{\partial z^{(1)}_{i,1}} =((p(y_{i}=1)-1(y_{i}=1))\cdot W^{(2)}_{1,1} +(p(y=2)-1(y=2))\cdot W^{(2)}_{1,2})\cdot 1(z^{(1)}_{i,1}\geq 0) \]
\[ \frac {\partial J}{\partial z^{(1)}_{i,2}} =\frac {\partial J}{\partial a^{(1)}_{i,2}}\cdot \frac {\partial a^{(1)}_{i,2}}{\partial z^{(1)}_{i,2}} =((p(y_{i}=1)-1(y_{i}=1))\cdot W^{(2)}_{2,1} +(p(y_{i}=2)-1(y_{i}=2))\cdot W^{(2)}_{2,2})\cdot 1(z^{(1)}_{i,2}\geq 0) \]
\[ \frac {\partial J}{\partial z^{(1)}_{i,3}} =\frac {\partial J}{\partial a^{(1)}_{i,3}}\cdot \frac {\partial a^{(1)}_{i,3}}{\partial z^{(1)}_{i,3}} =((p(y_{i}=1)-1(y_{i}=1))\cdot W^{(2)}_{3,1} +(p(y_{i}=2)-1(y_{i}=2))\cdot W^{(2)}_{3,2})\cdot 1(z^{(1)}_{i,3}\geq 0) \]
\[ \frac {\partial J}{\partial z^{(1)}_{i,4}} =\frac {\partial J}{\partial a^{(1)}_{i,4}}\cdot \frac {\partial a^{(1)}_{i,4}}{\partial z^{(1)}_{i,4}} =((p(y_{i}=1)-1(y_{i}=1))\cdot W^{(2)}_{4,1} +(p(y_{i}=2)-1(y_{i}=2))\cdot W^{(2)}_{4,2})\cdot 1(z^{(1)}_{i,4}\geq 0) \]
\[ \Rightarrow \frac {\partial J}{\partial z^{(1)}_{i}} =(\begin{bmatrix} p(y_{i}=1)-1(y_{i}=1) & p(y_{i}=2)-1(y_{i}=2) \end{bmatrix} \begin{bmatrix} W^{(2)}_{1,1} & W^{(2)}_{2,1} & W^{(2)}_{3,1} & W^{(2)}_{4,1}\\ W^{(2)}_{1,2} & W^{(2)}_{2,2} & W^{(2)}_{3,2} & W^{(2)}_{4,2} \end{bmatrix}) *\begin{bmatrix} \frac {\partial a^{(1)}_{i,1}}{\partial z^{(1)}_{i,1}}& \frac {\partial a^{(1)}_{i,2}}{\partial z^{(1)}_{i,2}}& \frac {\partial a^{(1)}_{i,3}}{\partial z^{(1)}_{i,3}}& \frac {\partial a^{(1)}_{i,4}}{\partial z^{(1)}_{i,4}} \end{bmatrix}\\ =(R^{1\times 2}\cdot R^{2\times 4})* R^{1\times 4} =R^{1\times 4} \]
\[ \Rightarrow \frac {\partial J}{\partial z^{(1)}_{i}} =(\begin{bmatrix} p(y_{i}=1)-1(y_{i}=1) & p(y_{i}=2)-1(y_{i}=2) \end{bmatrix} \begin{bmatrix} W^{(2)}_{1,1} & W^{(2)}_{2,1} & W^{(2)}_{3,1} & W^{(2)}_{4,1}\\ W^{(2)}_{1,2} & W^{(2)}_{2,2} & W^{(2)}_{3,2} & W^{(2)}_{4,2} \end{bmatrix}) * \begin{bmatrix} 1(z^{(1)}_{i,1}\geq 0) & 1(z^{(1)}_{i,2}\geq 0) & 1(z^{(1)}_{i,3}\geq 0) & 1(z^{(1)}_{i,4}\geq 0) \end{bmatrix}\\ =(R^{1\times 2}\cdot R^{2\times 4})\ast R^{1\times 4} =R^{1\times 4} \]
\[ \Rightarrow \frac {\partial J}{\partial z^{(1)}} =(\begin{bmatrix} p(y_{1}=1)-1(y_{1}=1) & p(y_{1}=2)-1(y_{1}=2)\\ \vdots & \vdots\\ p(y_{m}=1)-1(y_{m}=1) & p(y_{m}=2)-1(y_{m}=2) \end{bmatrix} \begin{bmatrix} W^{(2)}_{1,1} & W^{(2)}_{2,1} & W^{(2)}_{3,1} & W^{(2)}_{4,1}\\ W^{(2)}_{1,2} & W^{(2)}_{2,2} & W^{(2)}_{3,2} & W^{(2)}_{4,2} \end{bmatrix}) * \begin{bmatrix} 1(z^{(1)}_{1,1}\geq 0) & 1(z^{(1)}_{1,2}\geq 0) & 1(z^{(1)}_{1,3}\geq 0) & 1(z^{(1)}_{1,4}\geq 0)\\ \vdots & \vdots\\ 1(z^{(1)}_{m,1}\geq 0) & 1(z^{(1)}_{m,2}\geq 0) & 1(z^{(1)}_{m,3}\geq 0) & 1(z^{(1)}_{m,4}\geq 0) \end{bmatrix}\\ =\frac {\partial J}{\partial a^{(1)}} * 1(z^{(1)}\geq 0) =(R^{m\times 2}\cdot R^{2\times 4})\ast R^{m\times 4} =R^{m\times 4} \]
计算隐藏层权重向量的梯度
\[ \frac {\partial J}{\partial W^{(1)}_{1,1}} =\frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,1}}\cdot \frac {\partial z^{(1)}_{i,1}}{\partial W^{(1)}_{1,1}} =\frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=1)-1(y_{i}=1))\cdot W^{(2)}_{1,1} +(p(y_{i}=2)-1(y_{i}=2))\cdot W^{(2)}_{1,2})\cdot 1(z^{(1)}_{i,1}\geq 0)\cdot a^{(0)}_{i,1} \]
\[ \frac {\partial J}{\partial W^{(1)}_{1,2}} =\frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,2}}\cdot \frac {\partial z^{(1)}_{i,2}}{\partial W^{(1)}_{1,2}} =\frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=1)-1(y_{i}=1))\cdot W^{(2)}_{2,1} +(p(y_{i}=2)-1(y_{i}=2))\cdot W^{(2)}_{2,2})\cdot 1(z^{(1)}_{i,2}\geq 0)\cdot a^{(0)}_{i,1} \]
\[ \Rightarrow \frac {\partial J}{\partial W^{(1)}_{k,l}} =\frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,l}}\cdot \frac {\partial z^{(1)}_{i,l}}{\partial W^{(1)}_{k,l}} =\frac {1}{m}\sum_{i=1}^{m} ((p(y_{i}=1)-1(y_{i}=1))\cdot W^{(2)}_{l,1} +(p(y_{i}=2)-1(y_{i}=2))\cdot W^{(2)}_{l,2})\cdot 1(z^{(1)}_{i,l}\geq 0)\cdot a^{(0)}_{i,k} \]
\[ \Rightarrow \frac {\partial J}{\partial W^{(1)}} =\begin{bmatrix} \frac {\partial J}{\partial W^{(1)}_{1,1}} & \frac {\partial J}{\partial W^{(1)}_{1,2}} & \frac {\partial J}{\partial W^{(1)}_{1,3}} & \frac {\partial J}{\partial W^{(1)}_{1,4}}\\ \frac {\partial J}{\partial W^{(1)}_{2,1}} & \frac {\partial J}{\partial W^{(1)}_{2,2}} & \frac {\partial J}{\partial W^{(1)}_{2,3}} & \frac {\partial J}{\partial W^{(1)}_{2,4}}\\ \frac {\partial J}{\partial W^{(1)}_{3,1}} & \frac {\partial J}{\partial W^{(1)}_{3,2}} & \frac {\partial J}{\partial W^{(1)}_{3,3}} & \frac {\partial J}{\partial W^{(1)}_{3,4}} \end{bmatrix}\\ =\begin{bmatrix} \frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,1}}\cdot \frac {\partial z^{(1)}_{i,1}}{\partial W^{(1)}_{1,1}} & \frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,2}}\cdot \frac {\partial z^{(1)}_{i,2}}{\partial W^{(1)}_{1,2}} & \frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,3}}\cdot \frac {\partial z^{(1)}_{i,3}}{\partial W^{(1)}_{1,3}} & \frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,4}}\cdot \frac {\partial z^{(1)}_{i,4}}{\partial W^{(1)}_{1,4}}\\ \frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,1}}\cdot \frac {\partial z^{(1)}_{i,1}}{\partial W^{(1)}_{2,1}} & \frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,2}}\cdot \frac {\partial z^{(1)}_{i,2}}{\partial W^{(1)}_{2,2}} & \frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,3}}\cdot \frac {\partial z^{(1)}_{i,3}}{\partial W^{(1)}_{2,3}} & \frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,4}}\cdot \frac {\partial z^{(1)}_{i,4}}{\partial W^{(1)}_{2,4}}\\ \frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,1}}\cdot \frac {\partial z^{(1)}_{i,1}}{\partial W^{(1)}_{3,1}} & \frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,2}}\cdot \frac {\partial z^{(1)}_{i,2}}{\partial W^{(1)}_{3,2}} & \frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,3}}\cdot \frac {\partial z^{(1)}_{i,3}}{\partial W^{(1)}_{3,3}} & \frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i,4}}\cdot \frac {\partial z^{(1)}_{i,4}}{\partial W^{(1)}_{3,4}} \end{bmatrix}\\ =\frac {1}{m}\sum_{i=1}^{m} \begin{bmatrix} \frac {\partial J}{\partial z^{(1)}_{i,1}}\cdot \frac {\partial z^{(1)}_{i,1}}{\partial W^{(1)}_{1,1}} & \frac {\partial J}{\partial z^{(1)}_{i,2}}\cdot \frac {\partial z^{(1)}_{i,2}}{\partial W^{(1)}_{1,2}} & \frac {\partial J}{\partial z^{(1)}_{i,3}}\cdot \frac {\partial z^{(1)}_{i,3}}{\partial W^{(1)}_{1,3}} & \frac {\partial J}{\partial z^{(1)}_{i,4}}\cdot \frac {\partial z^{(1)}_{i,4}}{\partial W^{(1)}_{1,4}}\\ \frac {\partial J}{\partial z^{(1)}_{i,1}}\cdot \frac {\partial z^{(1)}_{i,1}}{\partial W^{(1)}_{2,1}} & \frac {\partial J}{\partial z^{(1)}_{i,2}}\cdot \frac {\partial z^{(1)}_{i,2}}{\partial W^{(1)}_{2,2}} & \frac {\partial J}{\partial z^{(1)}_{i,3}}\cdot \frac {\partial z^{(1)}_{i,3}}{\partial W^{(1)}_{2,3}} & \frac {\partial J}{\partial z^{(1)}_{i,4}}\cdot \frac {\partial z^{(1)}_{i,4}}{\partial W^{(1)}_{2,4}}\\ \frac {\partial J}{\partial z^{(1)}_{i,1}}\cdot \frac {\partial z^{(1)}_{i,1}}{\partial W^{(1)}_{3,1}} & \frac {\partial J}{\partial z^{(1)}_{i,2}}\cdot \frac {\partial z^{(1)}_{i,2}}{\partial W^{(1)}_{3,2}} & \frac {\partial J}{\partial z^{(1)}_{i,3}}\cdot \frac {\partial z^{(1)}_{i,3}}{\partial W^{(1)}_{3,3}} & \frac {\partial J}{\partial z^{(1)}_{i,4}}\cdot \frac {\partial z^{(1)}_{i,4}}{\partial W^{(1)}_{3,4}} \end{bmatrix}\\ =\frac {1}{m}\sum_{i=1}^{m} \begin{bmatrix} \frac {\partial J}{\partial z^{(1)}_{i,1}}\cdot a^{(0)}_{i,1} & \frac {\partial J}{\partial z^{(1)}_{i,2}}\cdot a^{(0)}_{i,1} & \frac {\partial J}{\partial z^{(1)}_{i,3}}\cdot a^{(0)}_{i,1} & \frac {\partial J}{\partial z^{(1)}_{i,4}}\cdot a^{(0)}_{i,1}\\ \frac {\partial J}{\partial z^{(1)}_{i,1}}\cdot a^{(0)}_{i,2} & \frac {\partial J}{\partial z^{(1)}_{i,2}}\cdot a^{(0)}_{i,2} & \frac {\partial J}{\partial z^{(1)}_{i,3}}\cdot a^{(0)}_{i,2} & \frac {\partial J}{\partial z^{(1)}_{i,4}}\cdot a^{(0)}_{i,2}\\ \frac {\partial J}{\partial z^{(1)}_{i,1}}\cdot a^{(0)}_{i,3} & \frac {\partial J}{\partial z^{(1)}_{i,2}}\cdot a^{(0)}_{i,3} & \frac {\partial J}{\partial z^{(1)}_{i,3}}\cdot a^{(0)}_{i,3} & \frac {\partial J}{\partial z^{(1)}_{i,4}}\cdot a^{(0)}_{i,3} \end{bmatrix}\\ =\frac {1}{m}\sum_{i=1}^{m} \begin{bmatrix} a^{(0)}_{i,1}\\ a^{(0)}_{i,2}\\ a^{(0)}_{i,3} \end{bmatrix} \begin{bmatrix} \frac {\partial J}{\partial z^{(1)}_{i,1}} & \frac {\partial J}{\partial z^{(1)}_{i,2}} & \frac {\partial J}{\partial z^{(1)}_{i,3}} & \frac {\partial J}{\partial z^{(1)}_{i,4}} \end{bmatrix} =\frac {1}{m}\sum_{i=1}^{m} (a^{(0)}_{i})^T\cdot \frac {\partial J}{\partial z^{(1)}_{i}} =\frac {1}{m} (a^{(0)})^T\cdot \frac {\partial J}{\partial z^{(1)}} =R^{3\times m}\cdot R^{m\times 4} =R^{3\times 4} \]
小结
TestNet网络的前向操作如下:
\[ z^{(1)} =a^{(0)}\cdot W^{(1)}+b^{(1)} \]
\[ a^{(1)}=relu(z^{(1)}) \]
\[ z^{(2)} =a^{(1)}\cdot W^{(2)}+b^{(2)} \]
\[ h(z^{(2)}) =\begin{bmatrix} p(y_{1}=1) & p(y_{1}=2) \\ \vdots & \vdots\\ p(y_{m}=1) & p(y_{m}=2) \end{bmatrix} \]
\[ J(z^{(2)})=(-1)\sum_{i=1}^{m} \sum_{j=1}^{2}\cdot 1(y_{m,j}=1)\ln p(y_{m,j}=1) \]
反向传播如下:
\[ \frac {\partial J}{\partial z^{(2)}} =\begin{bmatrix} p(y_{1}=1)-1(y_{1}=1) & p(y_{1}=2)-1(y_{1}=2)\\ \vdots & \vdots\\ p(y_{m}=1)-1(y_{m}=1) & p(y_{m}=2)-1(y_{m}=2) \end{bmatrix} \]
\[ \frac {\partial J}{\partial W^{(2)}} =\frac {1}{m} (a^{(1)})^{T}\cdot \frac {\partial J}{\partial z^{(2)}} \]
\[ \frac {\partial J}{\partial b^{(2)}} =\frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(2)}_{i}} \]
\[ \frac {\partial J}{\partial a^{(1)}} =\frac {\partial J}{\partial z^{(2)}}\cdot (W^{(2)})^T \]
\[ \frac {\partial J}{\partial z^{(1)}} =\frac {\partial J}{\partial a^{(1)}} * 1(z^{(1)}\geq 0) \]
\[ \frac {\partial J}{\partial W^{(1)}} =\frac {1}{m} (a^{(0)})^T\cdot \frac {\partial J}{\partial z^{(1)}} \]
\[ \frac {\partial J}{\partial b^{(1)}} =\frac {1}{m}\sum_{i=1}^{m} \frac {\partial J}{\partial z^{(1)}_{i}} \]
假设批量数据大小为\(m\),数据维数为\(D\),网络层数为\(L\)(\(1,2,...,l,...,L\)),输出类别为\(C\)
参考反向传导算法和神经网络反向传播的数学原理,设每层输入向量为残差\(\delta^{(l)}=\frac{\partial J(W, b)}{\partial z^{(l)}}\),用于表示该层对最终输出值的残差造成的影响;而最终输出值的残差\(\delta^{(L)}\)就是损失函数对输出层输入向量的梯度
前向传播执行步骤
层与层之间的操作就是输出向量和权值矩阵的加权求和以及对输入向量的函数激活(以relu为例)
\[ z^{(l)} = a^{(l-1)}\cdot W^{(l)}+b^{(l)} \\ a^{(l)} = relu(z^{(l)}) \]
输出层输出结果后,进行评分函数的计算,得到最终的计算结果(以softmax分类为例)
\[ h(z^{(L)}) =\begin{bmatrix} p(y_{1}=1) & \dots & p(y_{1}=C) \\ \vdots & \vdots & \vdots\\ p(y_{m}=1) & \dots & p(y_{m}=C) \end{bmatrix} =\begin{bmatrix} \frac {exp(z^{(2)}_{1,1})}{\sum exp(z^{(2)}_{1})} & \dots & \frac {exp(z^{(2)}_{1,C})}{\sum exp(z^{(2)}_{1})} \\ \vdots & \vdots & \vdots\\ \frac {exp(z^{(2)}_{m,1})}{\sum exp(z^{(2)}_{m})} & \dots & \frac {exp(z^{(2)}_{m,C})}{\sum exp(z^{(2)}_{m})} \end{bmatrix} \]
损失函数根据计算结果判断最终损失值(以交叉熵损失为例)
\[ J(z^{(L)})=(-1)\sum_{i=1}^{m} \sum_{j=1}^{2}\cdot 1(y_{m,j}=1)\ln p(y_{m,j}=1) \]
反向传播执行步骤
计算损失函数对于输出层输入向量的梯度(最终层残差)
\[ \delta^{(L)}= \frac {\partial J}{\partial z^{(L)}} =\begin{bmatrix} p(y_{1}=1)-1(y_{1}=1) & \dots & p(y_{1}=C)-1(y_{1}=C)\\ \vdots & \vdots & \vdots\\ p(y_{m}=1)-1(y_{m}=1) & \dots & p(y_{m}=C)-1(y_{m}=C) \end{bmatrix} \]
计算中间隐藏层的残差值(\(L-1,L-2,...1\))
\[ \delta^{(l)}= \frac{\varphi J}{\varphi z^{(l)}} =(\frac{\varphi J}{\varphi z^{(l+1)}}\cdot \frac{\varphi z^{(l+1)}}{\varphi a^{(l)}}) *\frac{\varphi a^{(l)}}{\varphi z^{(l)}} =(\delta^{(l+1)}\cdot (W^{(l+1)})^{T}) *1(z^{(l)}\geq 0) \]
完成所有的可学习参数(权值矩阵和偏置向量)的梯度计算
\[ \nabla_{W^{(l)}} J(W, b)= \frac {1}{m} (a^{(l-1)})^{T}\cdot \delta^{(l)}\\ \nabla_{b^{(l)}} J(W, b)= \frac {1}{m}\sum_{i=1}^{m} \delta^{(l)}_{i} \]
更新权值矩阵和偏置向量
\[ W^{(l)}=W^{(l)}-\alpha\left[\nabla W^{(l)}+\lambda W^{(l)}\right] \\ b^{(l)}=b^{(l)}-\alpha \nabla b^{(l)} \]